Enseñar las ecuaciones en educación primaria y secundaria siempre ha sido todo un reto, pero con esta formación tendrás todas las herramientas didácticas para que tu alumnado aprenda de forma profunda y divertida.
Antes de empezar con las ecuaciones en JUMP Math, hay que tener en cuenta un punto muy importante:
La verticalidad: En matemáticas no se trata de lo que doy en el curso, sino de tener una perspectiva vertical y saber de dónde vienen los estudiantes y a dónde van. Esta perspectiva, que puede abarcar desde Infantil hasta Bachillerato, ayuda a comprender cómo se van encadenando los conceptos y el proceso adquiere mucho más sentido.
El sentido algebraico
Álgebra o pensamiento algebráico
Cuando pensamos en álgebra pensamos en incógnitas, letras, variables y que allí comienza el álgebra. Sin embargo, más que hablar de álgebra, tendríamos que hablar de pensamiento algebraico. Somos capaces de pensar algebraicamente cuando, entre otras muchas cosas, podemos expresar de forma general las relaciones en lugar de referirnos a los objetos concretos que se relacionan. Esto, en muchos casos, supone el paso del sentido numérico al sentido algebraico.
El pensamiento algebráico implica representar, generalizar y formalizar patrones y regularidades en cualquier àrea de las matemáticas.
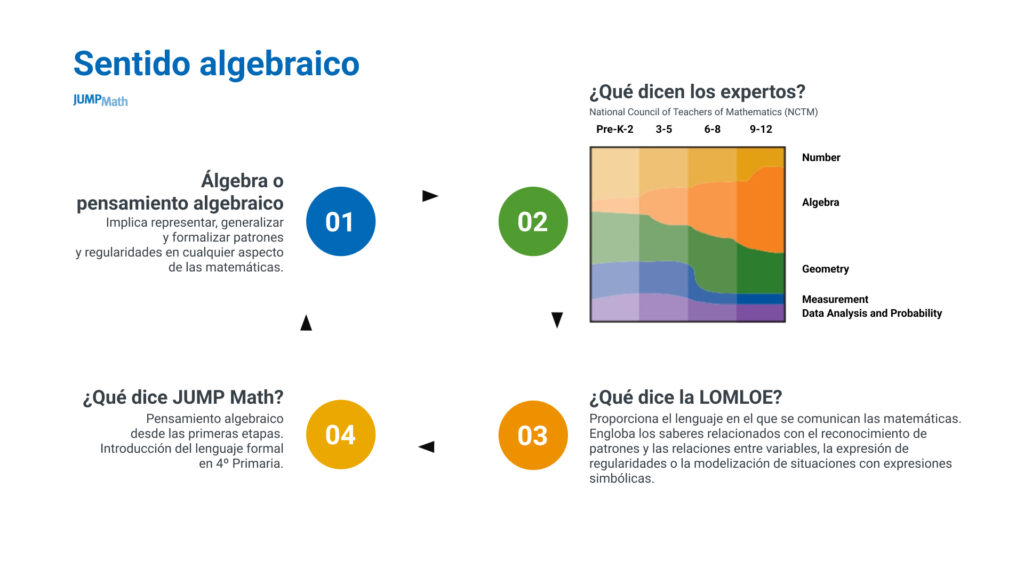
¿Qué dicen los expertos? – Las ecuaciones en JUMP Math
El National Council of Teachers of Mathematics (NCTM), dice que debemos empezar a trabajar el álgebra desde Infantil, ya que la búsqueda de los patrones o de la generalización es algo que se puede empezar a trabajar desde la primera infancia, adaptándose y adecuándose a las características específicas del desarrollo evolutivo del alumnado. Si bien no se puede trabajar el álgebra formal en cuanto a lenguaje, se puede trabajar utilizando materiales manipulativos. A medida que el alumnado se encuentra más inmerso en esto, el álgebra formal va ganando más espacio dentro de la enseñanza de las matemáticas.
¿Qué dice la LOMLOE? – Las ecuaciones en JUMP Math
La LOMLOE dice que el álgebra proporciona el lenguaje en el que se comunican las matemáticas.
También, engloba los saberes relacionados con el reconocimiento de patrones y las relaciones entre variables, la expresión de regularidades o la modelización de situaciones con expresiones simbólicas.
¿Qué dice JUMP Math?
JUMP Math coincide con los expertos de la NCTM en cuanto a que el pensamiento algebraico se empieza desde las primeras etapas, pero introduce su lenguaje formal en 4.º de Primaria
La importancia del vocabulario
Por ejemplo, es fundamental el trabajo de las igualdades en los cursos inferiores porque comprender el igual hará que comprendan mejor las ecuaciones.
Es importante ir precisando el vocabulario para facilitar al alumnado el entendimiento de las ecuaciones.
- Igualdad matemática: Es un enunciado que tiene dos expresiones equivalentes separadas por un signo igual. También se puede establecer una igualdad matemática numérica. Por ejemplo: 3+5 = 7+1.
- Ecuación: Igualdad matemática que solo se cumple para algunos valores de la variable.
- Incógnita: Letra o símbolo que tenemos que descubrir y cumple una condición.
- Variable: Letra o símbolo que puede tomar diversos valores numéricos.
El lenguaje algebraico
Aprender álgebra también es aprender un nuevo lenguaje, donde pueden aparecer letras o símbolos que me dicen que hay algo desconocido.

Los estudiantes pueden resolver este tipo de actividades, sin pensar en si es o no es una ecuación, ya que lo toman como si fuera un rompecabezas. Esto ayuda a trabajar y poner en marcha el pensamiento algebraico, el razonamiento y la prueba que la LOMLOE pide trabajar.
Cuando se construye el lenguaje se empieza por el sentido numérico y el sentido numérico transita hacia el sentido algebráico. Si el estudiante comprende que 4+3=7, entonces podrá encontrar el número que cumple la siguiente ecuación: 4+x=7

Así se trabaja el sentido numérico desde el lenguaje, introduciendo palabras como: más que, menos que, aumentado, dividido, añadido a, etc. que luego aparecerán en los ejercicios de álgebra.
Damos el salto a la expresión algebraica, aritmética generalizada
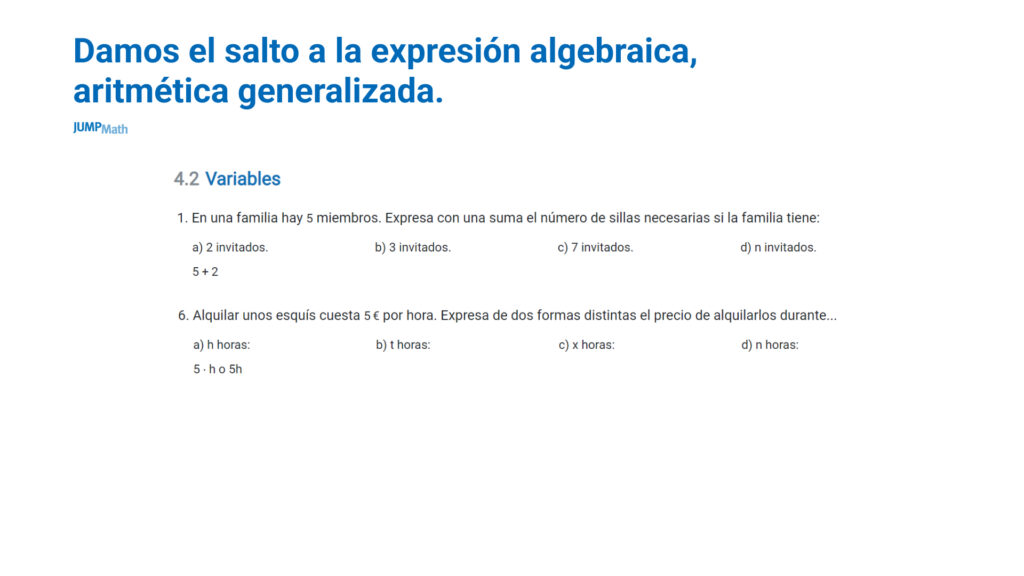
En el ejercicio anterior se propone al estudiante resolver distintas sumas como:
5+2, 5+3, 5+7 hasta dar el salto a la aritmética con 5+n. Si directamente se usan las letras los estudiantes no podrán encontrar el patrón de establecer que hay 5 miembros de la familia y se suman los invitados.
Así de a poco, van apareciendo las fórmulas.
Comprender expresiones algebraicas con significado
Una vez que ya se es capaz de construir expresiones algebraicas, es importante que esas expresiones algebraicas tengan un significado, para que el estudiante no escriba fórmulas sin entender qué está significando cada elemento de la fórmula.

En el ejercicio anterior se puede ver que la ecuación 5h+4 es 5 euros por cada hora más una tarifa fija de 4. Aunque para los adultos esto puede parecer evidente, para los estudiantes no lo es. Por eso, desde JUMP Math buscamos que haya procesos directos y procesos inversos.
- Proceso directo: Construir la fórmula
- Proceso inverso: Dada una fórmula, la comprendo
Es importante hacer los dos caminos para que el alumnado entienda qué significa la fórmula.
Una vez que el estudiante le ha dado significado, podemos avanzar a usar las letras con una intención. Ahora el estudiante ha descubierto que puede usar letras y que gracias a ello puede escribir cuestiones de forma general.
Por ejemplo:
Área del paralelogramo = base x altura (A = b x h) es una fórmula que se aplica para cualquier rectángulo sea cual sea su base y su altura y no para uno en concreto.
De esta forma, si quiere calcular el valor del área, basta con saber cuánto vale cada variable y, así sustituir y encontrar el valor del área. Entonces si b=2m y h=5m, el estudiante sustituye las letras por los números resuelve que 2m x 5m = 10m².
Es importante que los estudiantes vean que la posibilidad de utilizar letras es lo que permite escribir relaciones de forma general.
Si atendemos a la propuesta de la LOMLOE, comprobamos que se nos invita a establecer conexiones entre los diferentes sentidos matemáticos. Por eso, plantear cuestiones de álgebra en contextos geométricos puede resultar muy enriquecedor.
El lenguaje matemático se hace necesario para generalizar
Es importante que los alumnos tengan necesidad de los conocimientos matemáticos porque así el interés por los mismos está asegurado. Por eso hemos planteado el siguiente juego.

¿Es casualidad que el resultado para todos sea 3? No. El álgebra nos permitirá comprobarlo.
Al usar este tipo de ejercicios los estudiantes de alguna manera creen que estás “adivinando” y así descubrirán que lo que permite “adivinar” es precisamente el álgebra.
Hay dos maneras de formalizar esto: de manera pictórica o de manera simbólica.

Esto se puede trabajar con estudiantes de distintas edades dependiendo de la etapa y el curso en el que se imparte. Para estudiantes más pequeños se trabaja de forma pictórica y para estudiantes más grandes se trabaja de forma más simbólica.
Resolución de ecuaciones
Conceptos previos
En las siguientes actividades, no aparece ninguna ecuación. Sin embargo hay conceptos previos fundamentales para prepararlos para trabajar las ecuaciones.
- Propiedad de operaciones: Si el estudiante no tiene clara la propiedad de operaciones puede que el estudiante en el ejercicio 5 + 2 x 3, sume el 2 con el 5 sin haberse dado cuenta que previamente tiene que multiplicar. Lo mismo sucedería ante 2+3x, dirá que son 5x.

- Concepto de igualdad: Si el igual siempre lo usamos como resultado, los estudiantes no están entendiendo que 7 + 3 = 10 es una igualdad, sino que 10 es un resultado. Por eso es tan importante expresar las formas de todas las maneras posibles.

- Lo que es y lo que no es: Enseñar lo que es y lo que NO es una ecuación, hace que los estudiantes se hagan una idea completa de lo que esto significa.
Por ejemplo, aunque 9 = 4 + 5 sí es una igualdad, no es una ecuación porque no hay una incógnita que resolver.
7 – 5x, aunque hay una incógnita no es una ecuación porque no hay una igualdad.
2 – x = 4 es una ecuación porque sí hay una incógnita y una igualdad que resolver.
La construcción de las ecuaciones
JUMP Math plantea 3 etapas que evitan las rutinas mecánicas que hacen que los estudiantes memoricen sin entender. En su lugar se busca que comprendan lo que están haciendo y esto produzca un aprendizaje significativo.
- LO CONCRETO: Lo manipulativo, lo que se puede tocar. Se puede trabajar desde infantil usando los brazos como si fueran balanzas, balanzas de platillos, cajas con objetos, fichas para positivos y negativos, generando ecuaciones sencillas como: Dos fichas es igual a dos cajas. Usar lo manipulativo hace que los estudiantes trabajen desde lo concreto la construcción de ecuaciones.
- LO PICTÓRICO: Se produce a través de la representación. Se puede hacer de 3 modelos distintos:
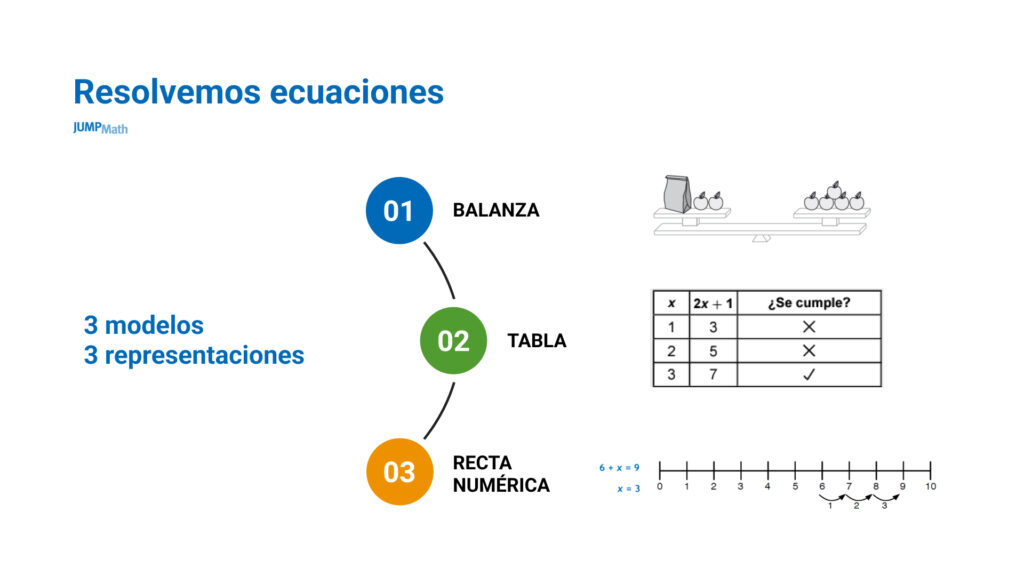
- LO SIMBÓLICO: Los estudiantes ya pasan a escribir con lenguaje algebraico. Operan con las letras y los números.
Si quieres saber más acerca de cómo trabajarlo, puedes ver la formación “Las ecuaciones de JUMP Math” en el apartado de Grabaciones.
Problemas de cintas y tablas
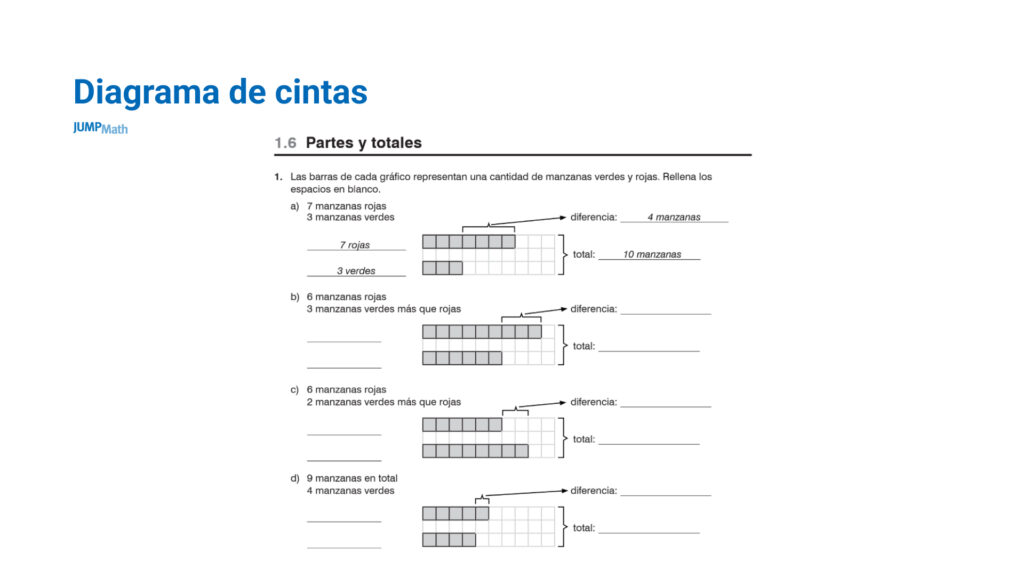
El apartado b) de la actividad sirve para introducir con números lo que luego haremos con letras. Este tipo de trabajos: más qué, menos qué, diferencia, prepara al alumnado para los problemas algebráicos que tendrán que resolver después.

En el ejercicio 1, la idea de “Isabel tiene 4 veces más adhesivos que Clara” da a entender que hay que multiplicar los adhesivos de Isabel. Sin embargo, un punto muy importante es que si se quisiera igualar a Isabel y Clara, no hay que multiplicar a Isabel, sino a Clara y entender esto puede resultar muy dificultoso para los estudiantes.

Por otro lado, problemas que aparecen de forma simbólica, se pueden resolver planteando una representación pictórica basándose en las balanzas, las cintas y que permitan al alumnado comprenderlo mejor.
Conexiones
Es muy importante situar las ecuaciones en todos los contextos que podamos.
- Contexto geométrico: Se puede adaptar a este contexto con situaciones sencillas que permiten entender que el álgebra también sirve para la geometría. Es una manera de que los estudiantes se sientan seguros con las ecuaciones y de conectar los sentidos que pide la LOMLOE.
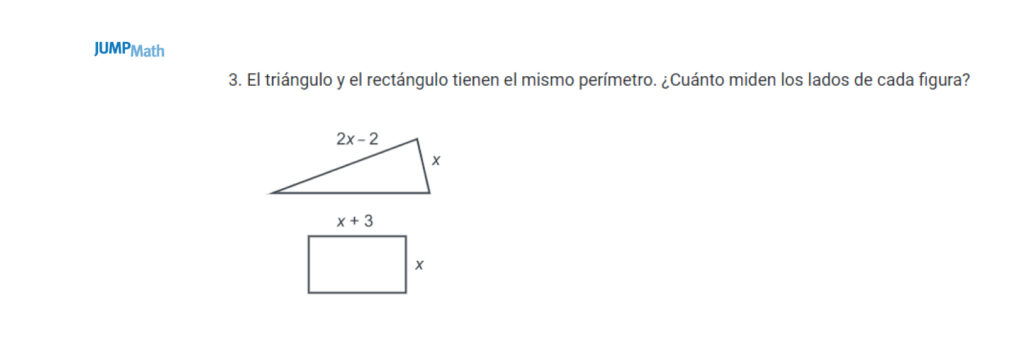
- Contexto aplicado a la vida cotidiana: Plantear problemas de la vida real donde el álgebra permite sacar conclusiones.

Esto pone al alumnado en un contexto de resolución de problemas en el que las ecuaciones permiten responder a todas las cuestiones que se plantean.
Resumen
- Sentido algebraico: Tiene que ver con el pensamiento algebráico que es aquel que permite generalizar y encontrar regularidades.
- Construcción del lenguaje: El álgebra también es un lenguaje que hay que aprender.
- Comprender las ecuaciones: Para poder comprender las ecuaciones hace falta manipular, representar y, por último, expresarlas en forma simbólica.
- Resolvemos problemas: Gracias a las ecuaciones puedo resolver problemas.
- Establecer conexiones: Solo comprendo las ecuaciones de manera global si las trabajo en los diferentes sentidos.