¿Sabías qué JUMP Math tiene una forma muy especial de enseñar la geometría? Profundiza en los conceptos geométricos en esta entrada al blog. 

La geometría: entre el sentido de la medida y el espacial

¿Qué dicen los expertos?

El National Council of Teachers of Mathematics (NCTM) 

La geometría es un área de las matemáticas que debe estudiarse en todas las etapas educativas por igual en cuanto al tiempo dedicado y cambiando la profundidad con la que se abordan los contenidos.»

LOMLOE: El sentido de la medida

Se caracteriza por la comprensión y comparación de atributos de los objetos del mundo natural. Hay que entender y elegir las unidades adecuadas para estimar, medir y comparar. 
Utilizar instrumentos adecuados para realizar mediciones, y comprender las relaciones entre magnitudes, utilizando la experimentación, son sus elementos centrales. 

En aula, en muchas ocasiones el trabajo de la geometría se reduce al cálculo de perímetros, áreas y volúmenes. Entonces se produce una aritmetización de la geometría. Es cierto que para poder comprender los cuerpos y las figuras necesitamos poder medir, pero no es lo único.

LOMLOE El sentido espacial

Es fundamental para comprender y apreciar los aspectos geométricos del mundo. Está constituido por la identificación, representación y clasificación de formas, el descubrimiento de sus propiedades y relaciones, la descripción de sus movimientos y el razonamiento con ellas.

No se trata de medir, sino de comprender, discriminar, clasificar. Esto es lo que nos permite comprender los objetos.

¿Qué dice JUMP Math?

JUMP Math tiene temas específicos de geometría que, además, están en conexión continua con otros contenidos. La propuesta es que la geometría sea el descubrimiento del plano y el espacio, para poder descubrir el entorno que nos rodea.

Aspectos generales de la geometría

Recursos para cada curso y para todos los cursos

Desde JUMP Math os proponemos una actividad para cada curso, pero también os invitamos a que penséis cómo las podéis utilizar en vuestra aula con otros contenidos, con otros sentidos. Son actividades que se pueden realizar de forma transversal puesto que sirven para trabajar cualquier aspecto de las matemáticas, y también de otras áreas del conocimiento y de forma vertical porque se pueden utilizar en cualquier curso ajustando el nivel de profundización.

1.º Primaria – ¿Qué cambia y qué permanece constante?, ¿qué caracteriza?

En matemáticas hay que estar muy atentos a qué cambia y qué permanece constante porque al final aquellas cosas que permanecen constantes pese a los cambios, son las que están caracterizando los objetos matemáticos con los que se está trabajando.

Supongamos que frente a la siguiente actividad, un estudiante solo marca los cuadrados que son blancos.

Un estudiante que solo marca los cuadrados blancos no es que no haya entendido la definición, es que ha sacado una conclusión errónea pero que está basada en su lógica. Quizá en la clase solo se le han presentado cuadrados, y por tanto él piensa que una característica que deben cumplir los cuadrados, es que son blancos. Por esto, es importante presentar diversidad de modelos en las actividades. Cuadrados con distintas posiciones, distintos colores, tamaños, etc. Por eso, cuando el estudiante hace mal la actividad hay que preguntarle: ¿qué criterio estás utilizando?

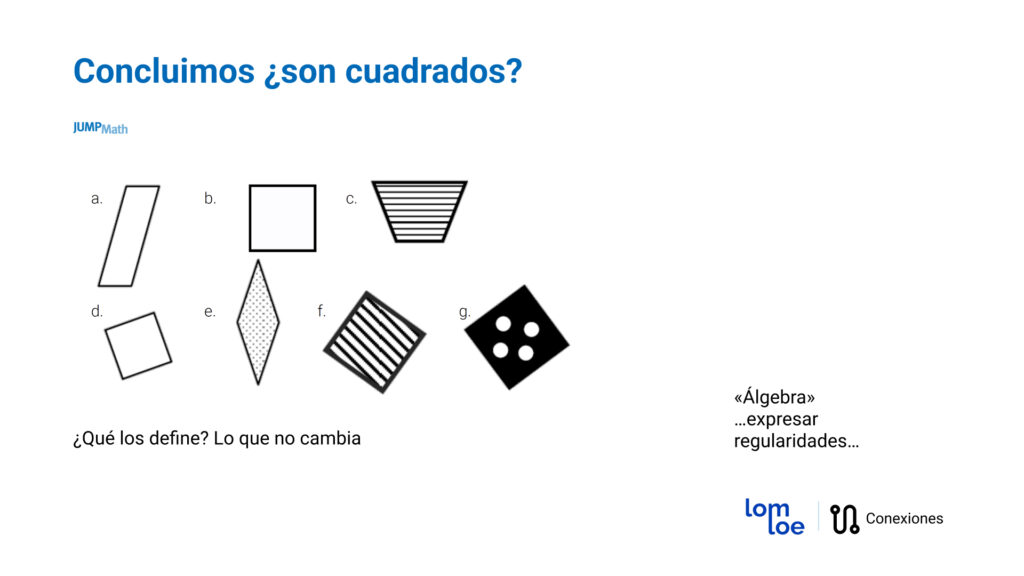
Es importante dejar claro que el color, el tamaño, la posición, no son características propias del cuadrado, para que los estudiantes comprendan cuáles sí son las características que lo definen.

Cuando un alumno puede sacar conclusiones de las regularidades que observa, estamos trabajando el sentido algebraico, por tanto es interesante exponerle ante estas cuestiones.

Entonces, si hacemos la pregunta: “¿qué cambia y que no?” los estudiantes se podrán dar cuenta que hay cosas que pueden cambiar (como el color, la posición y el tamaño) y hay cosas que no pueden cambiar (que sea un polígono cerrado de 4 lados iguales y tenga 4 ángulos rectos).

Esta misma actividad se podría hacer con cualquier otra figura geométrica.

2.º Primaria –  ¿Iguales o diferentes?

Frente a la pregunta: “¿Son iguales o diferentes?” los estudiantes entienden que son totalmente iguales o diferentes. Pero no comprenden que pueden ser en parte iguales o en parte diferentes.

En la siguiente imagen hay un rectángulo y un cuadrado. Si preguntamos “¿Son iguales o diferentes?” tendríamos que preguntarnos “¿En qué?”.

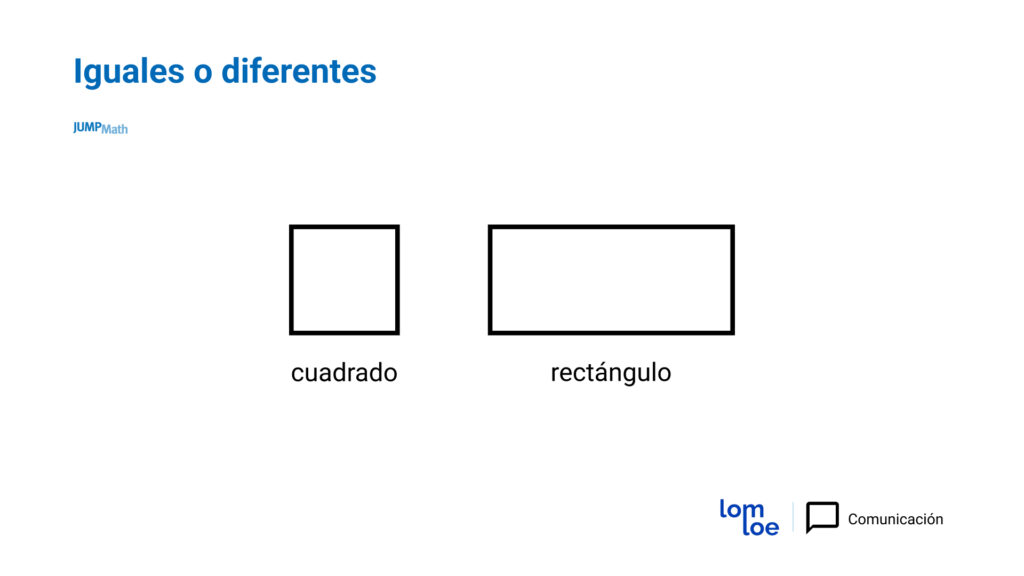
De esta forma los estudiantes podrán diferenciar que son iguales en que: son polígonos, tienen 4 lados rectos, 4 vértices, 4 ángulos rectos. 

Y que son diferentes en que: uno tiene 2 lados más largos y dos lados más cortos.

Este tipo de actividades son buenas para atender a la diversidad porque normalmente los estudiantes que tienen más dificultades tienen más vergüenza a intervenir porque, al ser preguntas cerradas o está bien o está mal. Sin embargo, en este tipo de actividades, no hay una única respuesta correcta y se lanzan a ver lo que ellos observan. Por ejemplo, si bien el color no es una característica propia de las figuras geométricas, podrían haber contestado que los dos son blancos.

Si vamos un paso más allá y analizamos las diagonales, podemos ver que al doblar el rectángulo por su diagonal, los lados no coinciden; en cambio sí coinciden en el cuadrado.

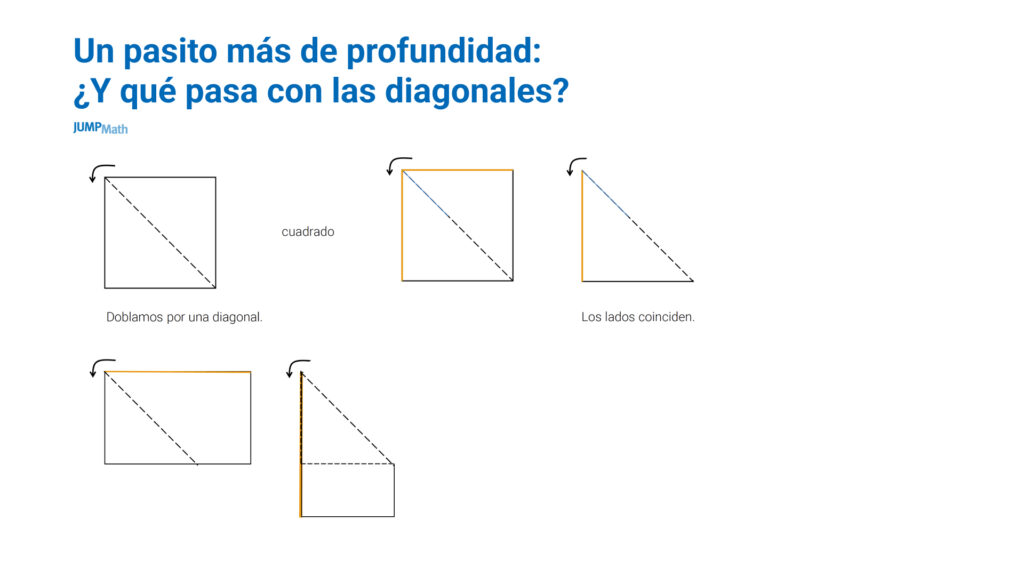
El docente debe llevar al aula todas las posibilidades para que a partir de lo que los alumnos digan, poder proponer un paso más para poder ganar profundidad.

3.º Primaria – Distinguimos dos conceptos muy relacionados

En general los estudiantes no distinguen muy bien entre el cálculo de área y el cálculo del perímetro. Entonces, si solo nos dedicamos a calcularlo, no se comprende bien qué les pasa a las figuras cuando les cambia el perímetro o les cambia el área y qué relación tienen estos dos conceptos.

Para ello, puedes ayudarte de las siguientes preguntas:

• ¿Cómo defino el área?, ¿y el perímetro?
• ¿Pueden dos figuras tener el mismo área y distinto perímetro? 
• ¿Pueden tener el mismo perímetro y distinta área?
• Construirlo con un mecano y transportar estas ideas al 3D.

Este tipo de actividades son importantes porque los estudiantes están acostumbrados a pensar que área y perímetro sean lo mismo. Sin embargo, al resolverlo y comprobarlo, podrán ver que, por ejemplo, pueden tener la misma área y distinto perímetro, y permitirles discriminar entre dos conceptos que son distintos.

Otras propuestas de JUMP Math para trabajar estos contenidos son:

• Realizar figuras con palillos para poder ir cambiándolos de lugar y contar el número de palillos que forman el contorno de las figuras.
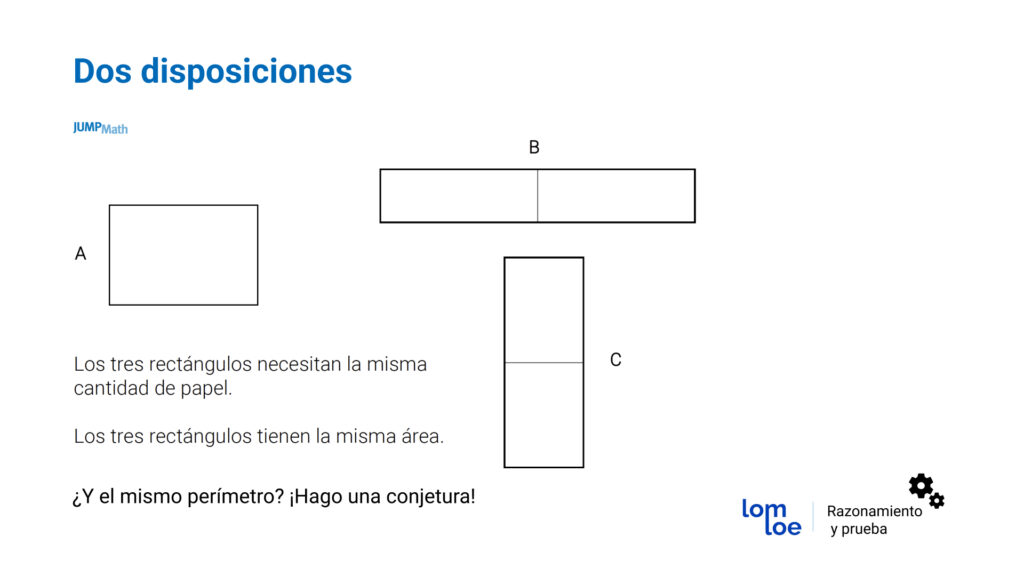
• Manipular un folio. Divides un folio en 4 partes iguales y usas 3. Una de ellas la dejas igual, otra la divides de nuevo en 2 verticalmente y otra la divides de nuevo en 2 horizontalmente. Si pegas las dos últimas como aparece en la figura, tienes en tus manos 3 rectángulos distintos: “Estos 3 rectángulos distintos, ¿tienen el mismo área?”, “¿tienen el mismo perímetro?”. Una vez que han conjeturado, comprueban y verifican si sus respuestas tenían sentido o no. Este tipo de actividades, también sirven para trabajar el razonamiento y la prueba que pide la LOMLOE.

4.º Primaria – Verdaderos y falsos

¿En qué contextos utilizar verdaderos y falsos? La respuesta es: ¡en todos!

• En el descubrimiento guiado.
• En la práctica individual.
• En las pruebas.
• En el trabajo por parejas.

Incluso podéis pedirles que inventen los verdaderos y falsos.

¿Qué competencias se trabajan con los verdaderos y falsos? 

• El razonamiento y la prueba: Porque tienen que argumentar su propio razonamiento.
• La comunicación: Porque hay que ser preciso y específico en lo que están contestando, para que el otro pueda entender el razonamiento.

Aquí te dejamos una actividad de JUMP Math para trabajar el verdadero o falso:

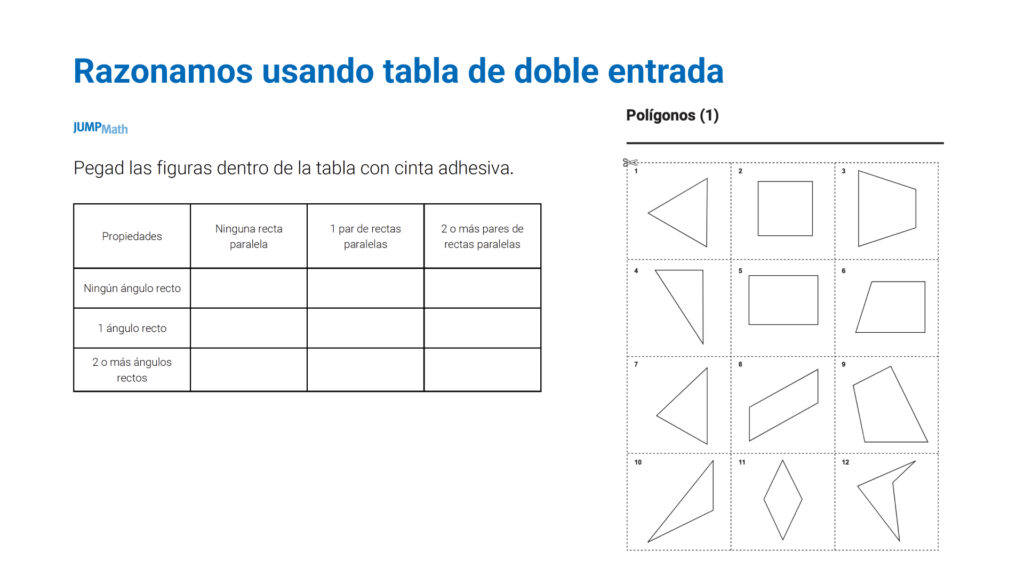
Para entrenar el verdadero o falso pueden empezar con estas frases:

• Existe alguno…
• No existe…
• La única que…
• Siempre…
• Hay únicamente…
• Hay más de un tipo que cumple…

5.º Primaria – Es la única que…

Este tipo de actividades promueve la participación del alumnado. Tiene un poco que ver con los verdaderos y falsos pero está planteado desde otro punto de vista.

El verdadero y falso tiene más que ver con razonamiento y prueba, y está actividad tiene más que ver con comunicar.

La actividad “Es la única que…” se trata de definir: “Esta figura es la única que cumple… (alguna condición)”.

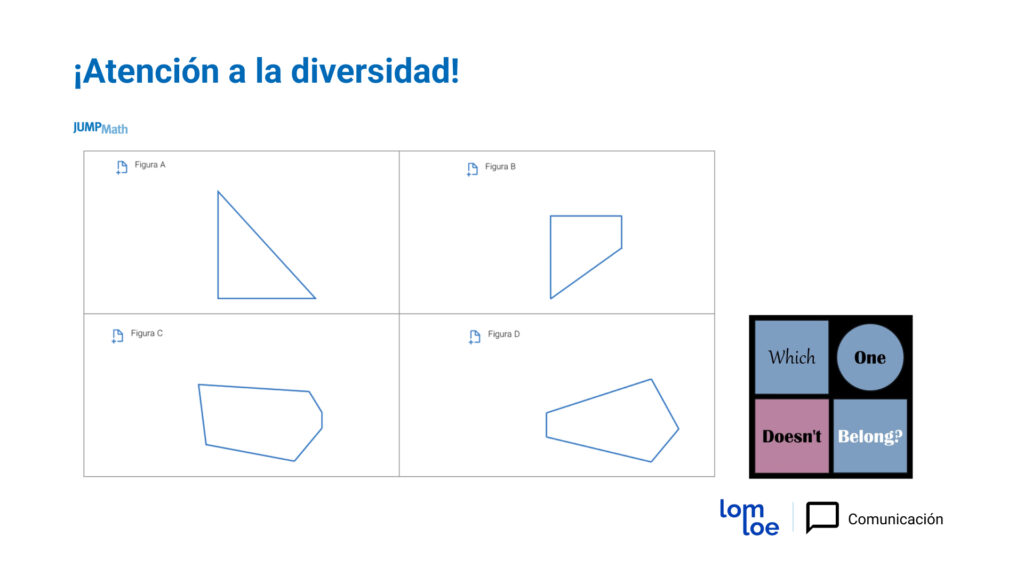
Por ejemplo (aunque hay más soluciones; lo importante es discutirlas):

• Figura A: La única figura con un eje de simetría y 3 lados (y 3 ángulos y 3 vértices).
• Figura B: La única figura con 2 ángulos rectos y 4 lados (añado, dos lados paralelos).
• Figura C: La única figura con 6 lados.
• Figura D: La única figura con 5 lados.

Se pueden añadir más figuras, más parecidas, en las que, por ejemplo, la única diferencia sean los ejes de simetría o la medida de los ángulos.

Podeis encontrar muchos ejemplos de esta actividad en Wich One Doesn’t Belong 

6.º Primaria – Un reto: memorizar lo mínimo. ¿Construímos las fórmulas?

Una de las dificultades que se encuentra en los cursos superiores es que se aprendan las fórmulas. Entonces para ello, es conveniente proponer retos.

Partiendo del área del rectángulo (A = b x h), ¿podría conseguir el área del romboide? Quizá los alumnos nos digan que ¡sí! porque lo único que debo hacer es recortar una parte y pegarla en otro lugar para conseguir un rectángulo y así ya poder usar la fórmula que conozco. De esta forma son ellos mismos los que descubren las fórmulas.

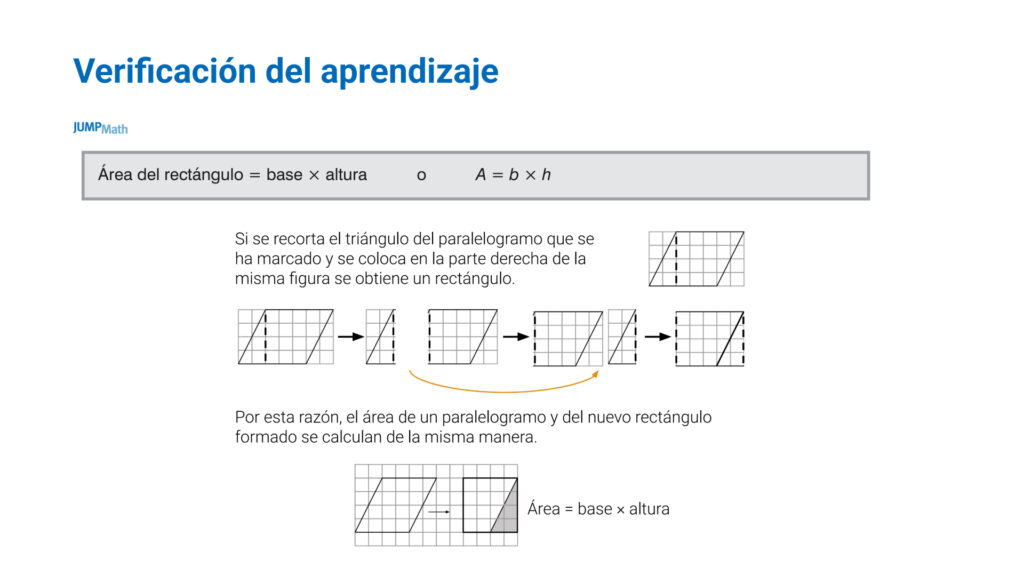
Lo mismo se puede realizar con un triángulo o con el trapecio, relacionándolo con el área del rectángulo.

Es muy diferente para los estudiantes darles una hoja con fórmulas que no tienen ningún sentido para ellos, a darles las figuras y que ellos puedan encontrar la relación entre las distintas fórmulas que aparecen en esa hoja.

1.º y 2.º ESO – ¿Quién es quién?

Deberán pensar en una de estas figuras y los demás, para descubrir la figura, pueden hacer preguntas que se respondan con «sí» o «no». Teniendo en cuenta las respuestas, hay que ir descartando figuras hasta descubrir de qué figura se trata.

Se puede realizar de forma grupal con la clase, o bien, en parejas.

Puedes encontrar más actividades como estas en Desmos.

¡Recuerda!

Para un aprendizaje motivador, es importante guíar a los estudiantes para que puedan descubrir los conocimientos.