Sabies que JUMP Math té una manera molt especial d’ensenyar la geometria? Aprofundeix en els conceptes geomètrics en aquesta entrada al bloc.

La geometria: entre el sentit de la mesura i l’espacial

Què diuen els experts?

El National Council of Teachers of Mathematics (NCTM) 

La geometria és una àrea de les matemàtiques que cal estudiar en totes les etapes educatives igual pel què fa al temps dedicat i canviant la profunditat amb què s’aborden els continguts.

LOMLOE: El sentit de la mesura

Es caracteritza per la comprensió i la comparació d’atributs dels objectes del món natural. Cal entendre i triar les unitats adequades per estimar, mesurar i comparar.
Utilitzar instruments adequats per mesurar, i comprendre les relacions entre magnituds, utilitzant l’experimentació, en són els elements centrals.

A l’aula, moltes vegades el treball de la geometria es redueix al càlcul de perímetres, àrees i volums. Aleshores es produeix una aritmetització de la geometria. És cert que per poder comprendre els cossos i les figures necessitem poder mesurar, però no és l’única cosa.

LOMLOE El sentit espacial

És fonamental per comprendre i apreciar els aspectes geomètrics del món. Està constituït per la identificació, representació i classificació de formes, el descobriment de les seves propietats i relacions, la descripció dels seus moviments i el raonament amb elles.

No es tracta de mesurar, sinó de comprendre, discriminar i classificar. Això és el que ens permet comprendre els objectes.

Què diu JUMP Math?

JUMP Math té temes específics de geometria que, a més a més, estan en connexió contínua amb altres continguts. La proposta és que la geometria sigui el descobriment del pla i l’espai, per poder descobrir l’entorn que ens envolta.

Aspectes generals de la geometria

Recursos per a cada curs i per a tots els cursos

Des de JUMP Math us proposem una activitat per a cada curs, però també us convidem a que penseu com les podeu utilitzar a la vostra aula amb altres continguts, amb altres sentits. Són activitats que es poden realitzar de forma transversal ja que serveixen per treballar qualsevol aspecte de les matemàtiques, i també d’altres àrees del coneixement i de forma vertical perquè es poden utilitzar a qualsevol curs ajustant el nivell d’aprofundiment.

1r Primària – Què canvia i què roman constant?, què caracteritza?

En matemàtiques cal estar molt atents a què canvia i què roman constant perquè al final aquelles coses que romanen constants malgrat els canvis, són les que estan caracteritzant els objectes matemàtics amb què s’està treballant.

Suposem que davant de la següent activitat, un estudiant només marca els quadrats que són blancs.

Un estudiant que només marca els quadrats blancs no és que no hagi entès la definició, és que n’ha tret una conclusió errònia però que està basada en la seva lògica. Potser a la classe només se li han presentat quadrats, i per tant ell pensa que una característica que han de complir els quadrats és que siguin blancs. Per això, és important presentar diversitat de models a les activitats. Quadrats amb diferents posicions, diferents colors, mides, etc. Quan l’estudiant fa malament l’activitat cal preguntar-li: quin criteri utilitzes?

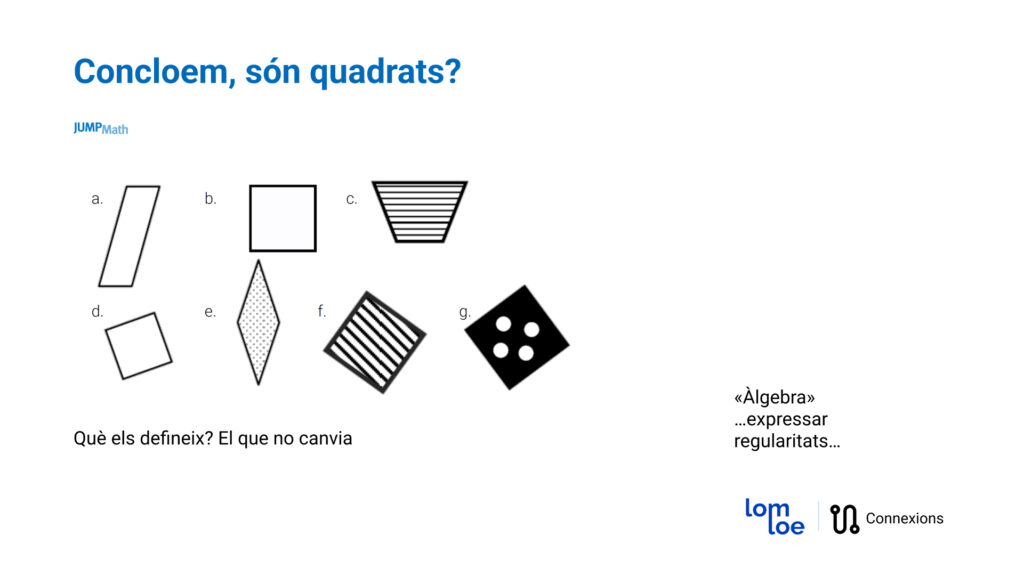
És important deixar clar que el color, la mida, la posició, no són característiques pròpies del quadrat, perquè els estudiants comprenguin quines sí que són les característiques que el defineixen.

Quan un alumne pot treure conclusions de les regularitats que observa, estem treballant el sentit algebraic, per tant és interessant exposar-ho davant d’aquestes qüestions.

Aleshores, si fem la pregunta: “què canvia i què no?” els estudiants es podran adonar que hi ha coses que poden canviar (com el color, la posició i la mida) i hi ha coses que no poden canviar (que sigui un polígon tancat de 4 costats iguals i tingui 4 angles rectes).

Aquesta mateixa activitat es podria fer amb qualsevol altra figura geomètrica.

2n Primària –  Iguals o diferents?

Davant la pregunta: “Són iguals o diferents?” els estudiants entenen que són totalment iguals o diferents. Però no comprenen que poden ser en part iguals o en part diferents.

A la següent imatge hi ha un rectangle i un quadrat. Si preguntem “Són iguals o diferents?” ens hauríem de preguntar “En què?”.

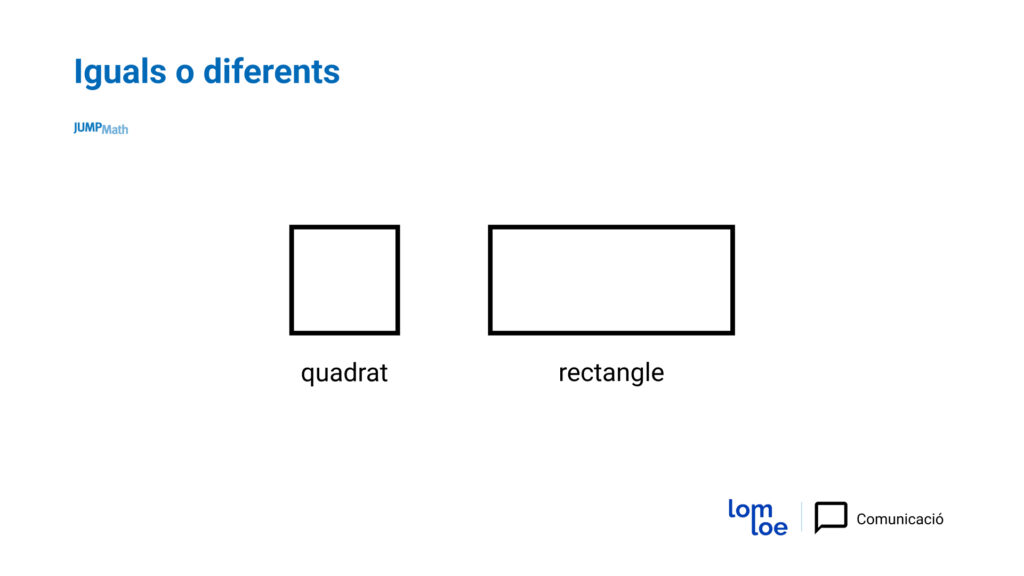
D’aquesta manera els estudiants podran diferenciar que són iguals i que són polígons, tenen 4 costats rectes, 4 vèrtexs i 4 angles rectes.

I que són diferents en què: un té 2 costats més llargs i dos costats més curts.

Aquest tipus d’activitats són bones per atendre la diversitat perquè normalment els estudiants que tenen més dificultats tenen més vergonya a intervenir perquè, en ser preguntes tancades o bé o malament. Tot i això, en aquest tipus d’activitats, no hi ha una única resposta correcta i es llancen a veure el que ells observen. Per exemple, si bé el color no és una característica pròpia de les figures geomètriques, podrien haver contestat que tots dos són blancs.

Si anem un pas més enllà i analitzem les diagonals, podem veure que en doblegar el rectangle pel diagonal, els costats no coincideixen; en canvi sí que coincideixen en el quadrat.

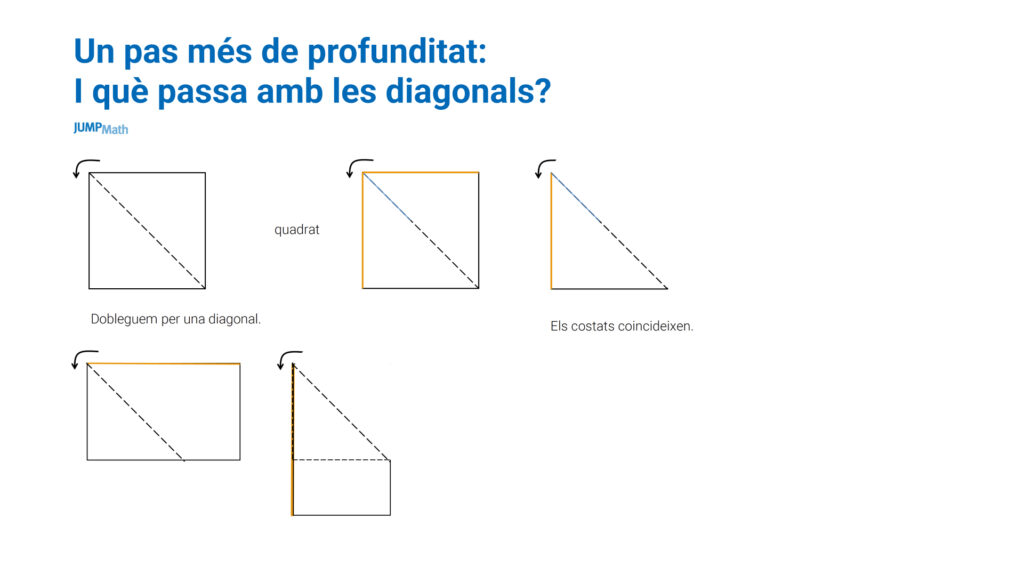
El docent ha de portar a l’aula totes les possibilitats perquè a partir del que diguin els alumnes, poder proposar un pas més per poder guanyar profunditat.

3r Primària – Distingim dos conceptes molt relacionats

En general, els estudiants no distingeixen gaire bé entre el càlcul d’àrea i el càlcul del perímetre. Aleshores, si només ens dediquem a calcular-ho, no es comprèn bé què els passa a les figures quan els canvia el perímetre o els canvia l’àrea i quina relació tenen aquests dos conceptes.

Per això, pots ajudar-te de les preguntes següents:

• Com defineixo l’àrea? I el perímetre?
• Poden dues figures tenir la mateixa àrea i un perímetre diferent?
• Poden tenir el mateix perímetre i àrea diferent?
• Construir-ho amb un mecano i transportar aquestes idees al 3D.

Aquests tipus d’activitats són importants perquè els estudiants estan acostumats a pensar que àrea i perímetre siguin el mateix. No obstant això, en resoldre-ho i comprovar-ho, podran veure que, per exemple, poden tenir la mateixa àrea i perímetre diferent, i permetre’ls discriminar entre dos conceptes que són diferents.

Altres propostes de JUMP Math per treballar aquests continguts són:

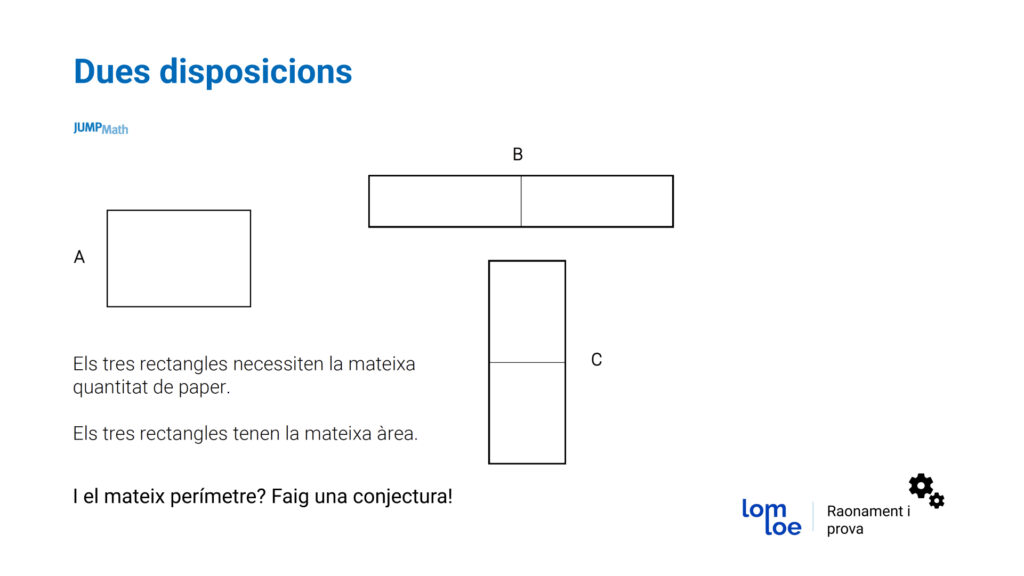
• Realitzar figures amb escuradents per poder anar canviant-los de lloc i comptar el nombre de escuradents que formen el contorn de les figures.
• Manipular un foli. Divideixes un foli en 4 parts iguals i utilitzes 3. Una d’elles la deixes igual, una altra la divideixes de nou en 2 verticalment i una altra la divideixes de nou en 2 horitzontalment. Si enganxes les dues últimes com apareix a la figura, tens a les teves mans 3 rectangles diferents: “Aquests 3 rectangles diferents, tenen la mateixa àrea?”, “tenen el mateix perímetre?”. Quan han conjecturat, comproven i verifiquen si les seves respostes tenien sentit o no. Aquests tipus d’activitats també serveixen per treballar el raonament i la prova que demana la LOMLOE.

4t Primària – Veritables i falsos

En quins contextos utilitzar veritables i falsos? La resposta és: en tots!

• Al descobriment guiat.
• A la pràctica individual.
• A les proves.
• A la feina per parelles.

Fins i tot podeu demanar-los que inventin els veritables i falsos.

Quines competències es treballen amb els veritables i falsos?

• El raonament i la prova: Perquè han d’argumentar el propi raonament.
• La comunicació: Perquè cal ser precís i específic en allò que estan contestant, perquè l’altre pugui entendre el raonament.

Aquí et deixem una activitat de JUMP Math per treballar el veritable o fals:

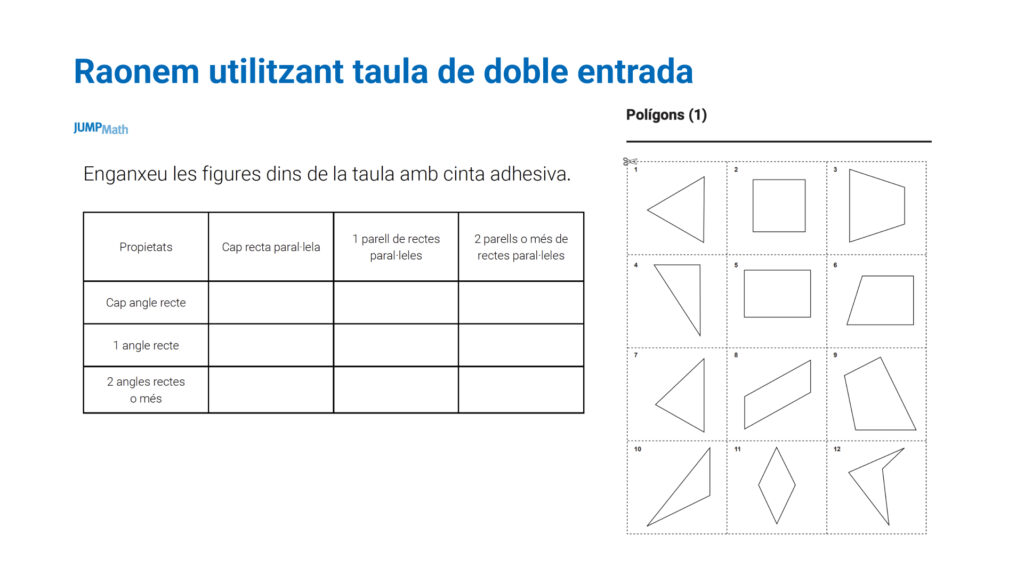
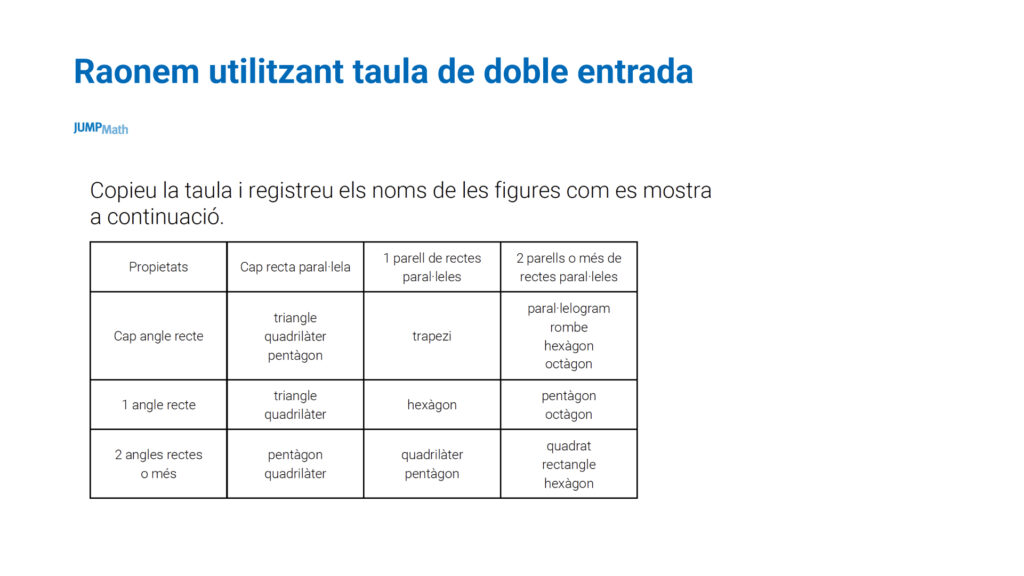
Per entrenar el veritable o fals poden començar amb aquestes frases:

• N’hi ha algun…
• No existeix…
• L’única…
• Sempre…
• Hi ha únicament…
• Hi ha més d’un tipus que compleix…

5è Primària – És l’única que…

Aquest tipus d’activitats promou la participació de l’alumnat. Té una mica a veure amb els veritables i falsos, però està plantejat des d’un altre punt de vista.

El veritable i fals té més a veure amb raonament i prova, i aquesta activitat té més a veure amb comunicar.

L’activitat “És l’única que…” es tracta de definir: “Aquesta figura és l’única que compleix… (alguna condició)”.

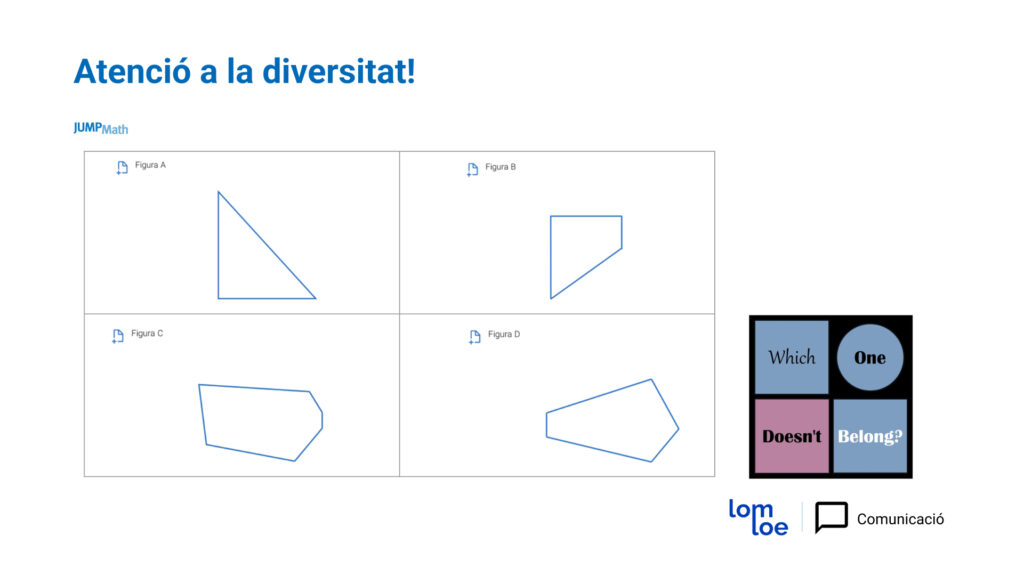
Per exemple (encara que hi ha més solucions; l’important és discutir-les):

• Figura A: L’única figura amb un eix de simetria i 3 costats (i 3 angles i 3 vèrtexs).
• Figura B: L’única figura amb 2 angles rectes i 4 costats (afegeixo, dos costats paral·lels).
• Figura C: L’única figura amb 6 costats.
• Figura D: L’única figura amb 5 costats.

S’hi poden afegir més figures, més semblants, en què, per exemple, l’única diferència siguin els eixos de simetria o la mida dels angles.

Podeu trobar molts exemples d’aquesta activitat a Which One Doesn’t Belong.

6è Primària – Un repte: memoritzar el mínim. Construïm les fórmules?

Una de les dificultats que trobem als cursos superiors és que s’aprenguin les fórmules. Aleshores per això, és convenient proposar reptes.

Partint de l’àrea del rectangle (A = b x h), podríeu aconseguir l’àrea del romboide? Potser els alumnes ens diran que sí! perquè l’únic que he de fer és retallar-ne una part i enganxar-la en un altre lloc per aconseguir un rectangle i així ja poder fer servir la fórmula que conec. D’aquesta manera, són ells mateixos els que descobreixen les fórmules.

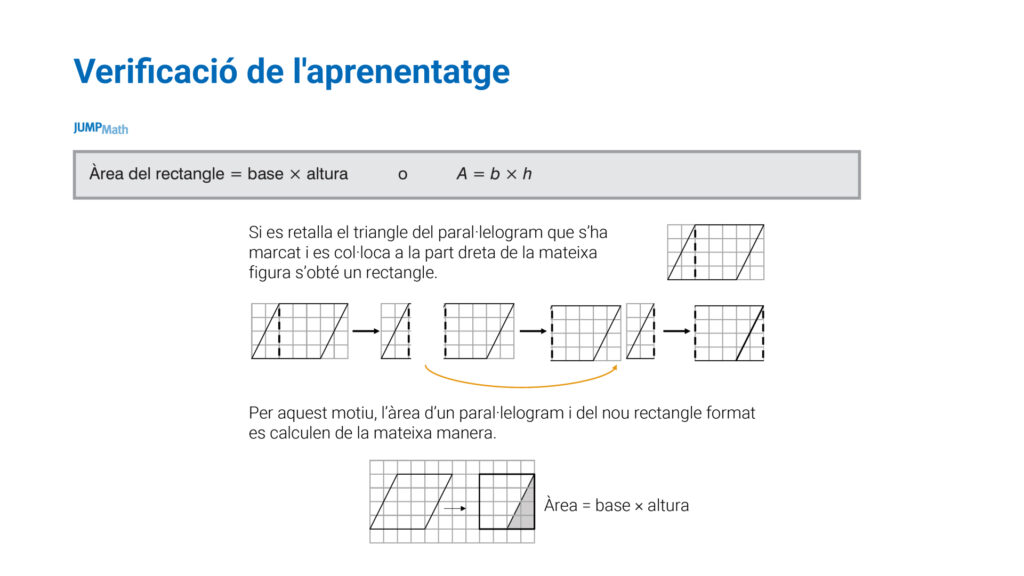
El mateix es pot fer amb un triangle o amb el trapezi, relacionant-lo amb l’àrea del rectangle.

És molt diferent per als estudiants donar-los un full amb fórmules que no tenen cap sentit per a ells, a donar-los les figures i que puguin trobar la relació entre les diferents fórmules que apareixen en aquest full.

1r i 2n ESO – Qui és qui?

Hauran de pensar en una d’aquestes figures i els altres, per descobrir la figura, poden fer preguntes que es responguin amb sí o no. Tenint en compte les respostes, cal anar descartant figures fins a descobrir de quina figura es tracta.

Es pot fer de forma grupal amb la classe, o bé, en parelles.

Pots trobar més activitats com aquestes a Desmos.

Recorda!

Per a un aprenentatge motivador, és important guiar els estudiants perquè puguin descobrir els coneixements.