En aquesta entrada al bloc us explicarem la diferència entre estructures i estratègies, el diagrama de cinta, els problemes de dos o més passos i molt més. Continua llegint!

Què és un problema?

Moltes vegades l’itinerari que es duu a terme a les classes de matemàtiques és el següent:

• S’hi expliquen conceptes fonamentals.
• Es fan exercicis bàsics.
• Es fan problemes contextualitzats.

Moltes vegades, aquests problemes, se’ls anomena problemes però no suposen un repte, no són més que una operació contextualitzada. És a dir, si jo llegeixo un exercici i automàticament sé què he de fer, no és un problema perquè no suposa un repte. És més aviat un exercici amb un context afegit.

D’altra banda, també és molt comú que aquests exercicis contextualitzats es facin al final del tema, quan ja s’han explicat els exercicis bàsics. És així com moltes vegades, els qui són capaços de fer els exercicis bàsics, després també són capaços de fer els exercicis contextualitzats, però els que no han estat capaços de fer els exercicis, tampoc són capaços de fer els exercicis contextualitzats.

Vegem algunes definicions de què és un problema:

“…resoldre un problema és trobar un camí allà on no es coneixia prèviament cap camí, trobar la manera de sortejar un obstacle, aconseguir la finalitat desitjada, que no és aconseguible de forma immediata, utilitzant els mitjans adequats”

(Polya,1980)

“Es parla de resoldre problemes, en lloc de simples exercicis, quan l’estudiant aconsegueix solucionar una situació problemàtica donada, contextualitzada o no, sense que se li hagi indicat un procediment que cal seguir.”

(BBCC Matemàtica, 2012)

A què ens referim a JUMP Math quan parlem de problemes?

Un problema:

• Posseeix interrogants.
• No es pot donar resposta immediata, perquè ni tan sols se sap d’entrada quin camí cal seguir.
• Requereix una reflexió.
• Presa de decisions.
  – Passos a seguir.
  – Coneixements a aplicar.

Resoldre un problema porta temps, ja que en no saber quin camí seguir i haver de reflexionar-hi, no el puc resoldre de manera immediata.

Les principals dificultats en la resolució de problemes

Aquí tenim uns problemes clàssics què habitualment han d’enfrontar els alumnes.

És important destacar que allò que en un curs és un problema perquè els alumnes no tenen encara els coneixements necessaris per resoldre’l de forma automàtica pot ser un exercici rutinari en cursos superiors. Per tant, de vegades un mateix enunciat pot ser alhora un problema o alhora no ser-ho depenent de qui s’hi enfronti.

L’alumnat pot trobar dificultats a l’hora de resoldre’l, ja sigui per la gestió de l’enunciat, per no trobar l’estratègia que cal seguir, perquè s’hi relacionen quantitats que no saben com relacionar-los, etc.

A l’hora de resoldre problemes:

• Alumnat: Apareixen dificultats pels ritmes d’aprenentatge i per la comprensió lectora dels estudiants. Per atendre les dificultats de ritmes d’aprenentatge es poden fer preguntes que permetin l’alumnat aprofundir en les parts del problema que li suposen una dificultat.
• Professorat: Pretén que hi hagi una resposta ràpida i eficaç, però cal que hi hagi reflexió i és molt difícil que hi hagi respostes. D’altra banda, el docent vol arribar a tothom, però es pot arribar a tothom però no a tothom alhora ja que cada estudiant té el seu propi ritme d’aprenentatge.
• Fites: Moltes vegades el problema són les fites, ja que el docent vol que l’alumnat sigui autònom, que utilitzi el raonament i que es diverteixi, i això no sempre passa.
• Bones pràctiques: Algunes bones pràctiques davant d’aquests escenaris poden ser:
  – Adaptar l’enunciat espaiant les frases i dividint-ne les inscripcions.
  – Utilitzant material manipulatiu.

Què proposa JUMP Math per a la resolució de problemes?

A l’hora de resoldre problemes:

Evitar:

• Associar paraules a operacions: És molt habitual a classe de matemàtiques dir per exemple: “Cada vegada que apareix la paraula “diferència” cal restar”, però l’única cosa que fomenta és la mecanització de les respostes i no fomenta la comprensió. A més, produeix errors en l’aprenentatge ja que per exemple si el problema diu: “La diferència entre l’edat de la Maria i la del Lluc és 5 anys, sabent que el Lluc és el menor i té 12 anys, quants en té la Maria?” En aquest cas, cal sumar en lloc de restar encara que aparegui la paraula diferència.

Fomentar:

• Incorporar dibuixos i representacions.
• Comunicar solucions entre companys: per veure quines diferències hi ha entre les solucions i quines estratègies s’han fet servir.
• Utilitzar materials: Per facilitar el pas del concret a allò abstracte.

L’objectiu principal com a docents és que els estudiants pensin i reflexionin.

JUMP Math proposa 3 fases:

• Fase concreta: fase manipulativa on es treballa amb materials.
• Fase pictòrica: on es pot representar.
• Fase simbòlica: on es pot expressar en operacions.

Podem plantejar un problema als estudiants, només donant-los alguna d’aquestes representacions:

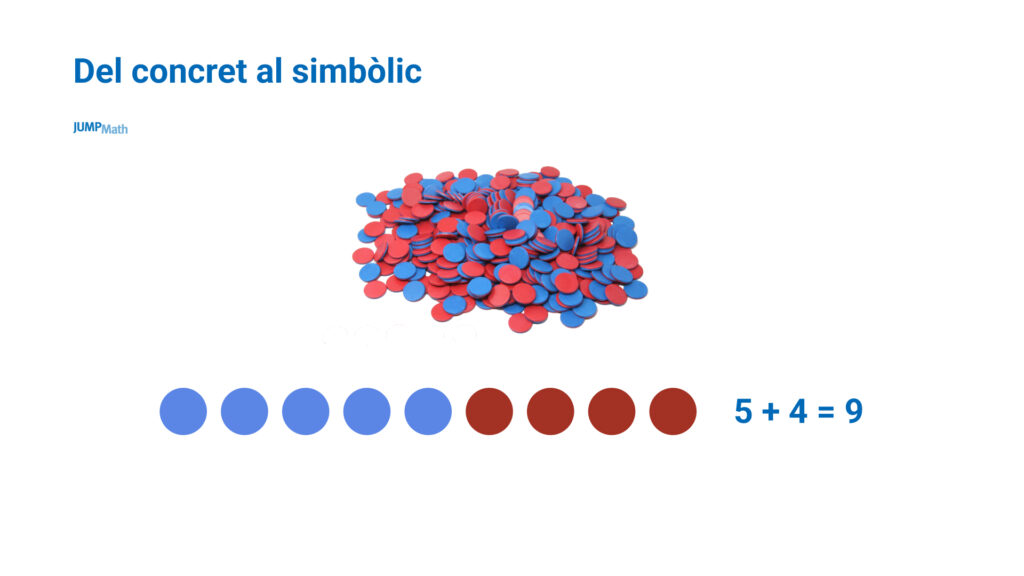
Quin problema podríem proposar amb aquestes combinacions?

• El Joan té 5 fitxes, entre el Joan i el Tomás tenen 9, quantes fitxes té el Tomás?
• El Joan té una fitxa més que el Tomàs. El Tomàs té 4 fitxes. Quantes fitxes tenen entre tots dos?
• El Joan té una fitxa més que el Tomàs. En total sumen 9 fitxes. Quantes fitxes té el Tomás?

També és interessant fer el procés invers, donar als estudiants representacions i que ells plantegin el problema.

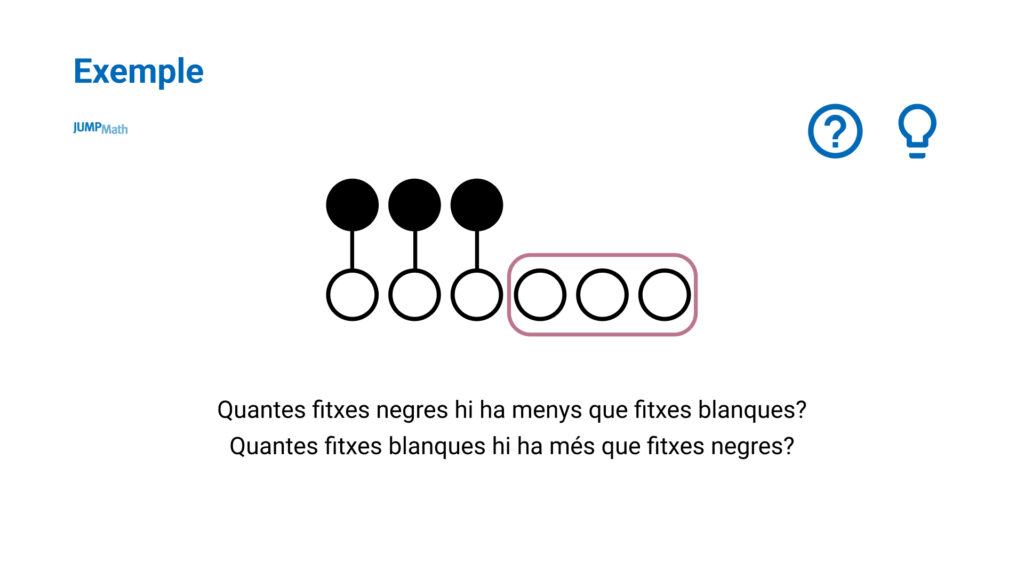
Oferir diferents tipus de representacions ordenades de diferents maneres també ajuda a donar-los idees perquè ells mateixos creïn els seus propis problemes i que puguin utilitzar-les per resoldre’ls.

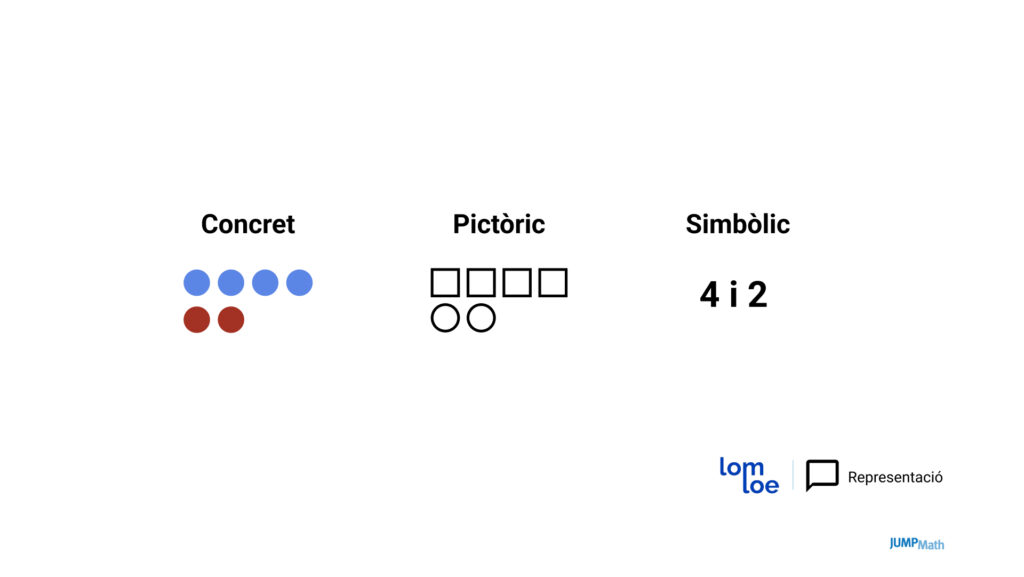
Allò pictòric simplifica els problemes

En alguns casos, la representació pictòrica ajuda que els estudiants puguin resoldre el problema de manera molt més fàcil que plantejar l’operació.

JUMP Math et dona la clau per a la resolució de problemes:

“Aïllar estratègies concretes i centrar-s’hi”

És a dir, cal pensar quines estratègies et van bé per a aquest problema. Tot i això, les estratègies de vegades són una mica genèriques, aleshores, cal plantejar estructures.

Què proposa JUMP Math?

Organitzar l’ensenyament de manera que:

• Es plantegin problemes amb context diferent, però mateixa estructura i es presentin junts perquè els estudiants puguin veure què tenen en comú i què tenen diferent.
• Es plantegin problemes amb el mateix context però diferent estructura i es presentin junts. Això és important per saber què és fonamental i què és superflu en el problema.

Utilitzar i comparar diferents apropaments al problema:

• Aprendre de les diferents respostes a un problema.
• Han de distingir entre similituds superficials (utilitzar pastanagues o caramels) i similituds profundes relacionades amb l’estructura matemàtica.

L’ús de les estructures a JUMP Math

En aquest cas s’utilitzarà la paraula “estructura” com a “representació”. És a dir, “quina representació permetrà resoldre de manera satisfactòria el problema?”.

Si jo no conec estructures o representacions que serveixin per resoldre problemes, no tindré les eines bàsiques per resoldre’ls.

JUMP Math ofereix diferents estructures per posar en joc i treballar-los. A la sessió d’avui en treballarem dos:

Diagrama part – tot:

Són diagrames on apareix un total i una divisió del total en dues o més parts. Es pot representar amb nombres o de manera pictòrica.

En quines situacions podem fer servir el diagrama?

• Verificació de la comprensió. Correcte o incorrecte?

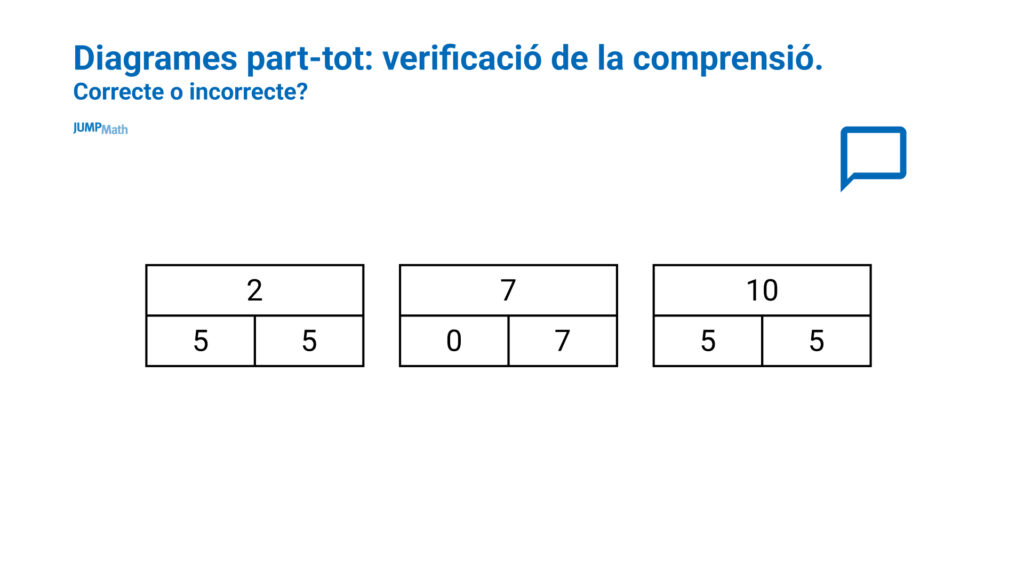
• Relació entre els components: La incògnita pot ser la part o el tot perquè depenent de quina sigui la incògnita s’utilitzarà una operació o una altra.

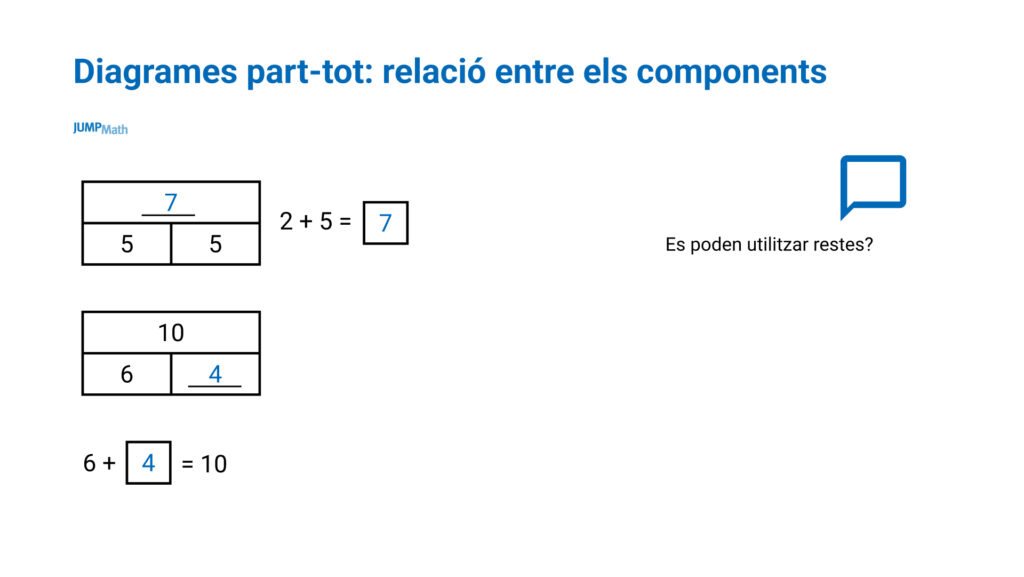
Això mateix es pot utilitzar per a l’ESO:

Diagrames de cinta:

Es caracteritzen perquè cadascuna de les parts són iguals.

Els diagrames de cintes solen servir en aquells problemes en què es comparen quantitats i es caracteritzen perquè a cada tros de la cinta li correspon una quantitat fixa.

També es poden fer servir per a problemes de fraccions:

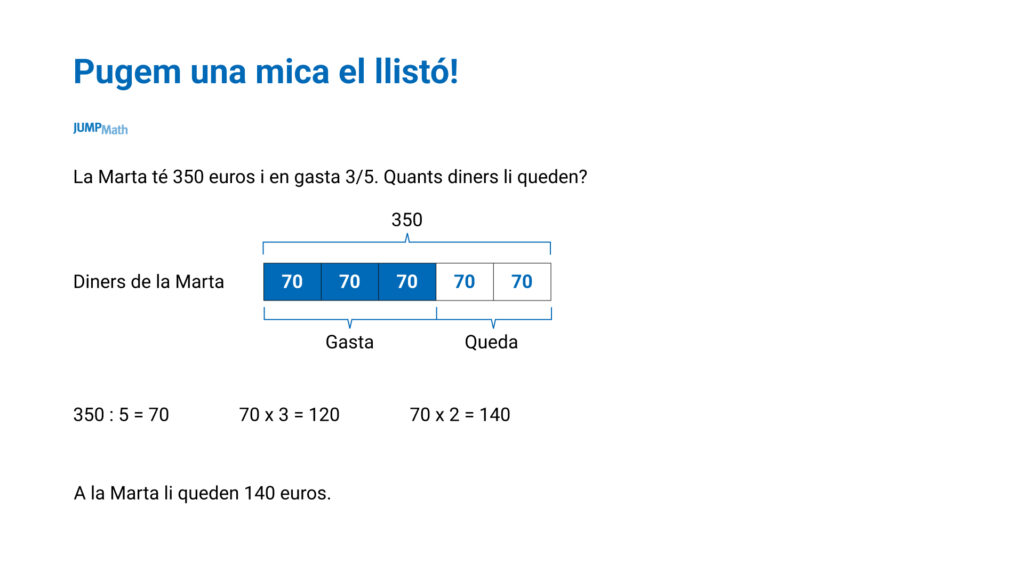
També es poden complicar encara més i al diagrama donar el que val la part en lloc de donar-los el valor total.

D’aquesta manera podreu respondre totes les preguntes que el docent faci:

• Quants ous ha fet servir per a les truites?
• Quants ous ha fet servir per als pastissos?
• Quants ous més ha fet servir per fer els pastissos que per fer les truites?

El mateix es pot fer en els problemes de percentatges:

I es poden fer servir per argumentar:

Per exemple:

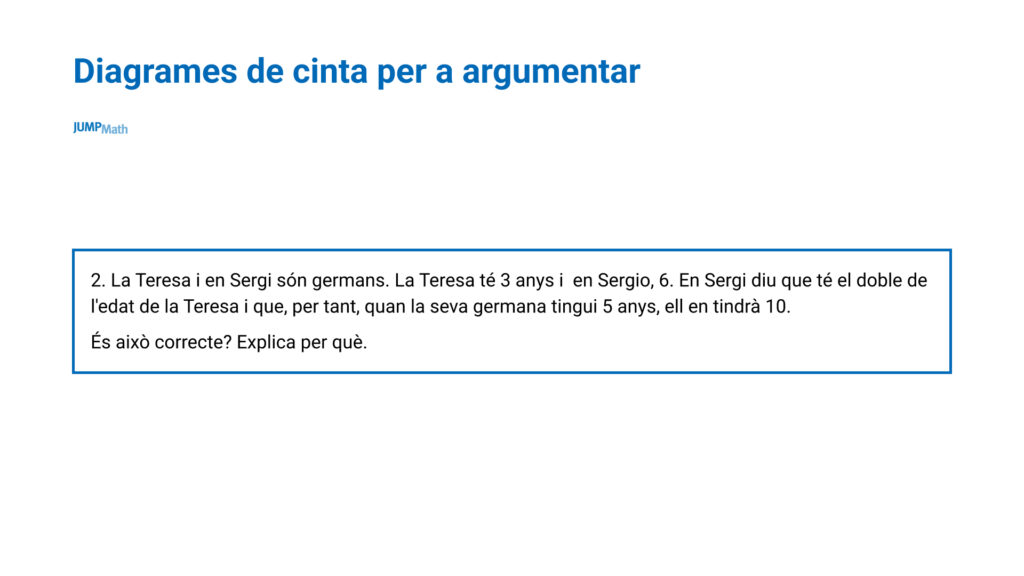
Resum

1. La resolució de problemes és fonamental en l’aprenentatge de les matemàtiques. No és un bloc a part. Els estudiants han d’estar sempre resolent reptes i problemes.
2. No és una tasca fàcil ni per a l’alumnat ni per al professorat perquè resoldre reptes requereix temps i reflexió.
3. Val la pena abordar-la mitjançant instruments, representacions o estratègies que l’alumnat integri per a tota la vida. Quan un alumne comprèn bé aquestes estructures, les pot fer servir en molts contextos de la vida quotidiana.
4. És important que l’alumnat sigui conscient de l’existència d’aquestes estratègies i del procés d’aprenentatge.
5. És important que l’alumnat conegui estructures que pugui utilitzar per resoldre els problemes que se li plantegen.

Quan els estudiants es fan competents en l’ús de les estructures, són molt més capaços d’argumentar-ne el raonament, de resoldre problemes, d’enfrontar-se a nous reptes perquè senten que saben on s’han de recolzar.

Us facilitem unes targetes de resolució de problemes per fomentar la feina autònoma de l’alumne. La idea és que l’alumne realitzi cadascuna de les accions i passi la targeta de banda a banda per poder fer sense ajuda del professor tots els passos

Descarrega ara el material manipulatiu per treballar tot allò après a classes!