En esta entrada al blog te contaremos la diferente entre estructuras y estrategias, el diagrama de cinta, los problemas de dos o más pasos y mucho más. ¡Sigue leyendo!
¿Qué es un problema?
Muchas veces el itinerario que se lleva a cabo en las clases de matemáticas es el siguiente:
- Se explican conceptos fundamentales.
- Se hacen ejercicios básicos.
- Se realizan problemas contextualizados.
Muchas veces, a esos problemas, se los llama problemas pero no suponen un reto, no son más que una operación contextualizada. Es decir, si yo leo un ejercicio y automáticamente sé lo que tengo que hacer, no es un problema porque no supone un reto. Es más bien, un ejercicio con un contexto añadido.
Por otro lado, también es muy común que estos ejercicios contextualizados se realicen al final del tema, cuándo ya se han explicado los ejercicios básicos. Es así como muchas veces, quienes son capaces de hacer los ejercicios básicos, luego también son capaces de hacer los ejercicios contextualizados, pero los que no han sido capaces de hacer los ejercicios, tampoco son capaces de hacer los ejercicios contextualizados.
Veamos algunas definiciones de qué es un problema:
“…resolver un problema es encontrar un camino allí donde no se conocía previamente camino alguno, encontrar la forma de sortear un obstáculo, conseguir el fin deseado, que no es conseguible de forma inmediata, utilizando los medios adecuados”
(Polya,1980)
“Se habla de resolver problemas, en lugar de simples ejercicios, cuando el estudiante logra solucionar una situación problemática dada, contextualizada o no, sin que se le haya indicado un procedimiento a seguir.”
(BBCC Matemática, 2012)
¿A qué nos referimos en JUMP Math cuando hablamos de problemas?
Un problema:
- Posee interrogantes.
- No se puede dar respuesta inmediata, porque ni siquiera se sabe de entrada qué camino hay que seguir.
- Requiere reflexión.
- Toma de decisiones.
- Pasos a seguir.
- Conocimientos a aplicar.
Resolver un problema lleva tiempo, ya que al no saber qué camino seguir y tener que reflexionar sobre ello, no puedo resolverlo de forma inmediata.
Las principales dificultades en la resolución de problemas
Aquí tenemos unos problemas clásicos a los que habitualmente se tienen que enfrentar los alumnos.

Es importante destacar que lo que en un curso es un problema porque los alumnos no tienen aún los conocimientos necesarios para resolverlo de forma automática puede ser un ejercicio rutinario en cursos superiores. Por lo tanto a veces un mismo enunciado puede ser a la vez un problema o a la vez no serlo dependiendo de quién se enfrente a él.
El alumnado puede encontrar dificultades a la hora de resolverlo, ya sea por la gestión del enunciado, por no encontrar la estrategia a seguir, porque se relacionan cantidades que no saben cómo relacionarlos, etc.
A la hora de resolver problemas:
- Alumnado: Aparecen dificultades por los ritmos de aprendizaje y por la comprensión lectora de los estudiantes. Para atender las dificultades de ritmos de aprendizaje se puede hacer preguntas que permitan al alumnado profundizar en las partes del problema que le suponen una dificultad.
- Profesorado: Pretende que haya una respuesta rápida y eficaz, sin embargo es necesario que haya reflexión y es muy difícil que haya respuestas. Por otro lado, el docente quiere llegar a todos y todas, sin embargo, se puede llegar a todos pero no a todos a la vez ya que cada estudiante tiene su propio ritmo de aprendizaje.
- Metas: Muchas veces el problema son las metas, ya que el docente quiere que el alumnado sea autónomo, que utilice el razonamiento y que se diviertan, y eso no siempre ocurre.
- Buenas prácticas: Algunas buenas prácticas frente a estos escenarios pueden ser:
– Adaptar el enunciado espaciando las frases y dividiendo las inscripciones.
– Utilizando material manipulativo.
¿Qué propone JUMP Math para la resolución de problemas?
A la hora de resolver problemas:
Evitar:
- Asociar palabras a operaciones: Es muy habitual en clase de matemáticas decir por ejemplo: “Cada vez que aparece la palabra “diferencia” hay que restar”, sin embargo lo único que fomenta es la mecanización de las respuestas y no fomenta la comprensión. Además, produce errores en el aprendizaje ya que por ejemplo si el problema dice: «La diferencia entre la edad de María y la de Lucas es 5 años, sabiendo que Lucas es el menor y tiene 12 años, ¿cuántos tiene María?» En este caso, hay que sumar en lugar de restar aunque aparezca la palabra diferencia.
Fomentar:
- Incorporar dibujos y representaciones.
- Comunicar soluciones entre compañeros: para ver que diferencias hay entre las soluciones y qué estrategias se han utilizado.
- Usar materiales: Para facilitar el pasaje de lo concreto a lo abstracto.
El objetivo principal como docentes es que los estudiantes piensen y reflexionen.
JUMP Math propone 3 fases:
- Fase concreta: fase manipulativa dónde se trabaja con materiales.
- Fase pictórica: dónde se puede representar.
- Fase simbólica: dónde se puede expresar en operaciones.
Podemos plantear un problema a los estudiantes, únicamente dándoles alguna de estas representaciones:
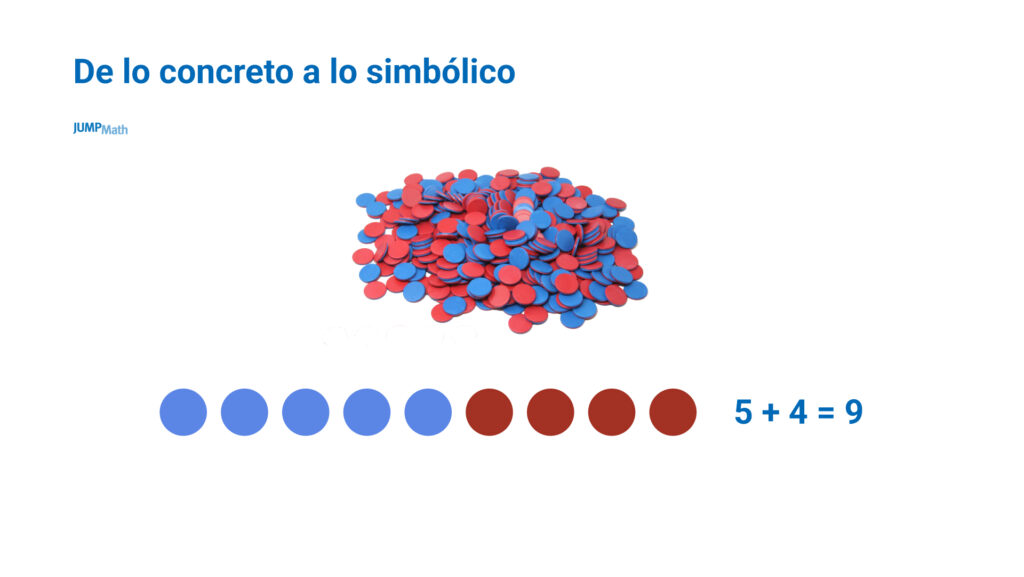
¿Qué problema podríamos proponer a partir de estas combinaciones?
- Juan tiene 5 fichas, entre Juan y Tomás tienen 9, ¿cuántas fichas tiene Tomás?.
- Juan tiene una ficha más que Tomás. Tomás tiene 4 fichas. ¿Cuántas fichas tienen entre los dos?
- Juan tiene una ficha más que Tomás. En total suman 9 fichas. ¿Cuántas fichas tiene Tomás?
También es interesante hacer el proceso inverso, dar a los estudiantes representaciones y que ellos planteen el problema.
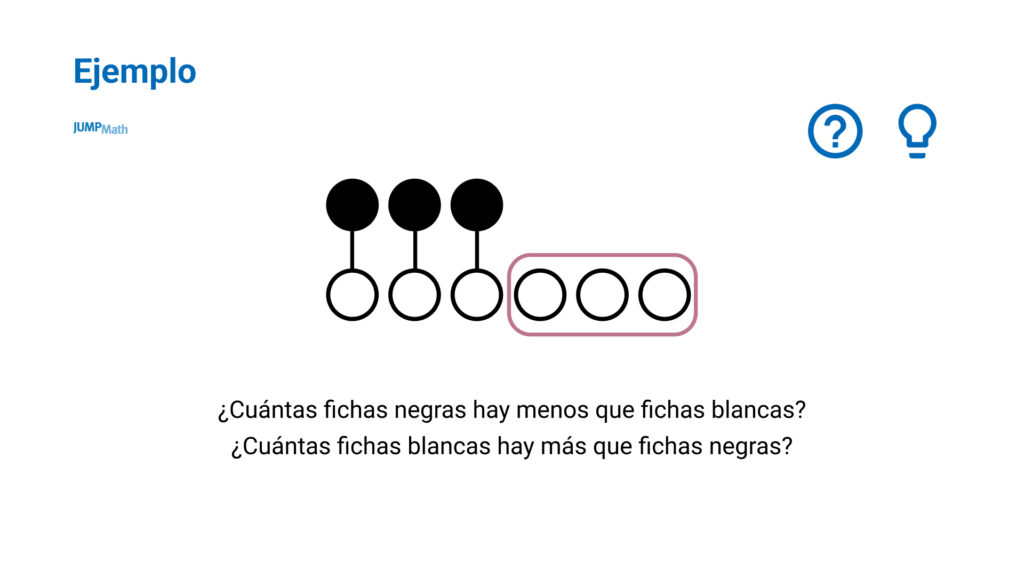
Ofrecer distintos tipos de representaciones ordenadas de diferentes maneras también ayuda a darles ideas para que ellos mismos creen sus propios problemas y que puedan utilizarlas para resolverlos.
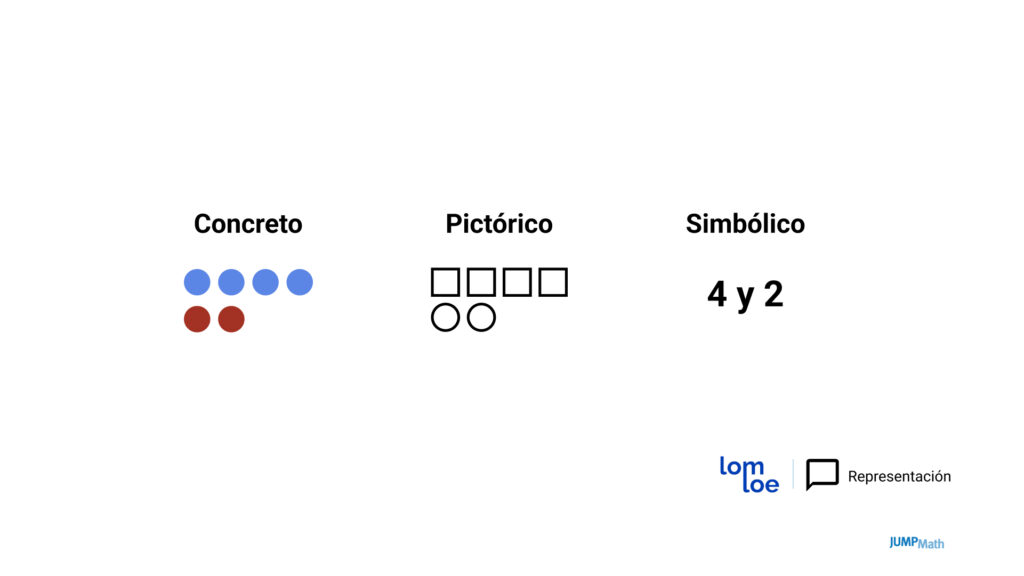
Lo pictórico simplifica los problemas
En algunos casos, la representación pictórica ayuda a que los estudiantes puedan resolver el problema de forma mucho más fácil que plantear la operación.
JUMP Math te da la clave para la resolución de problemas:
“Aislar estrategias concretas y centrarse en ellas”
Es decir que hay que pensar qué estrategias te van bien para ese problema. Sin embargo, las estrategias a veces son un poco genéricas, entonces, hay que plantear estructuras.
¿Qué propone JUMP? Math?
Organizar la enseñanza de manera que:
- Se planteen problemas con distinto contexto pero misma estructura y se presenten juntos para que los estudiantes puedan ver qué tienen en común y qué tienen distinto.
- Se planteen problemas con mismo contexto pero diferente estructura y se presenten juntos. Esto es importante para saber qué es fundamental y qué es superfluo en el problema.
Usar y comparar diferentes acercamientos al problema:
- Aprender de las diferentes respuestas a un problema.
- Deben distinguir entre similitudes superficiales (usar zanahorias o caramelos) y similitudes profundas relacionadas con la estructura matemática.
El uso de las estructuras en JUMP Math
En este caso se utilizará la palabra “estructura” como “representación”. Es decir, “¿qué representación va a permitir resolver de manera satisfactoria el problema?”.
Si yo no conozco estructuras o representaciones que sirvan para resolver problemas, no tendré las herramientas básicas para poder resolverlos.
JUMP Math ofrece distintas estructuras para poner en juego y trabajarlos. En la sesión de hoy trabajaremos dos:
Diagramar parte – todo:
Son diagramas dónde aparece un total y una división de ese total en dos o más partes. Se puede representar con número o de forma pictórica.
¿En qué situaciones podemos utilizar el diagrama?
- Verificación de la comprensión. ¿Correcto o incorrecto?
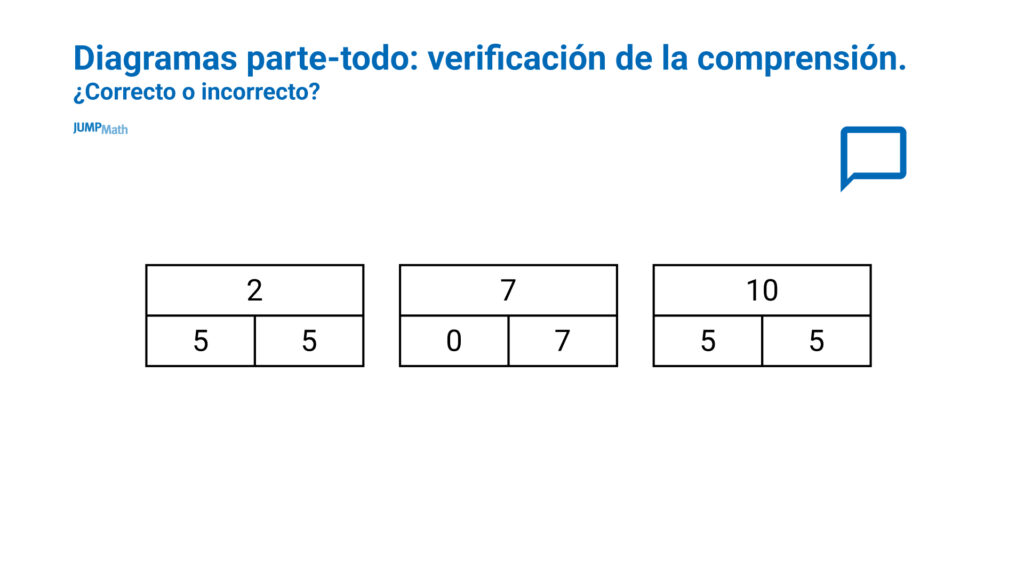
- Relación entre los componentes: La incógnita puede ser la parte o el todo, para que dependiendo de cuál sea la incógnita se utilizará una operación u otra.
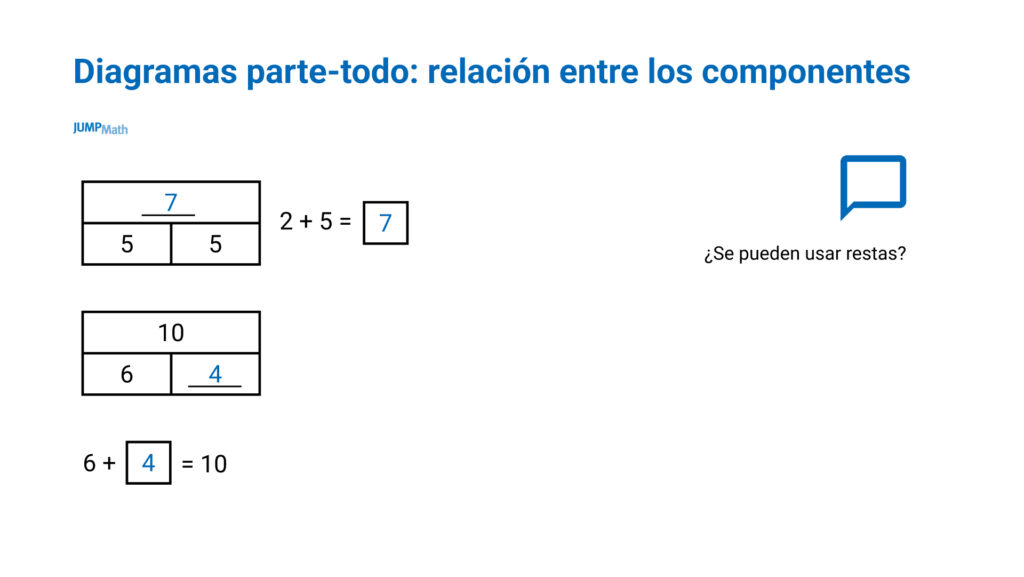
Esto mismo se puede utilizar para la ESO:


Diagramas de cinta
Se caracterizan por que cada una de las partes son iguales.

Los diagramas de cintas suelen servir en aquellos problemas en los que se comparan cantidades y se caracterizan porque a cada trozo de la cinta le corresponde una cantidad fija.
También se pueden usar para problemas de fracciones:
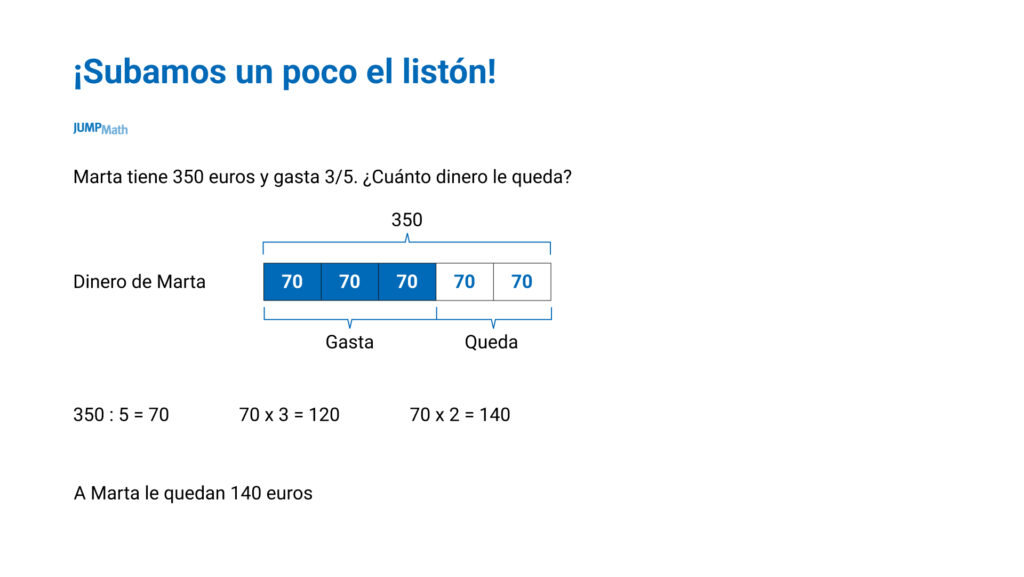
También se pueden complejizar aún más y en el diagrama dar lo que vale la parte en lugar de darles el valor total.

De esta forma podrá responder todas las preguntas que el docente haga:
- ¿Cuántos huevos ha usado para las tortillas?
- ¿Cuántos huevos ha usado para los pasteles?
- ¿Cuántos huevos más ha usado para hacer los pasteles que para hacer las tortillas?
Lo mismo se puede hacer en los problemas de porcentajes:
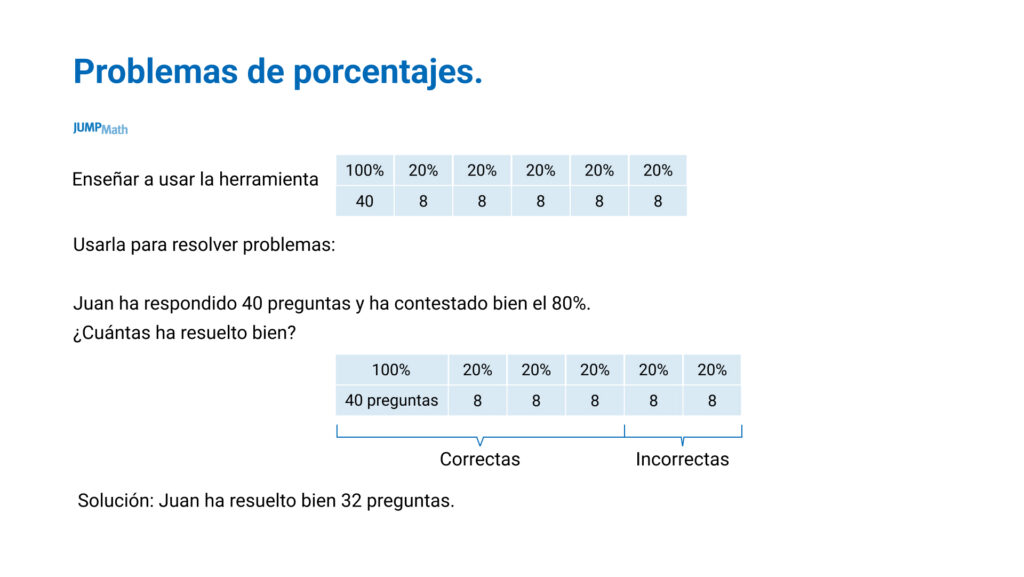
Y se pueden usar para argumentar:
Por ejemplo:

Resumen
- La resolución de problemas es fundamental en el aprendizaje de las matemáticas. No es un bloque aparte. Los estudiantes deben estar siempre resolviendo retos y problemas.
- No es una tarea fácil ni para el alumnado ni para el profesorado porque resolver retos requiere de tiempo y reflexión.
- Merece la pena abordarla a través de instrumentos, representaciones o estrategias que el alumnado integre para toda la vida. Cuando un alumno comprende bien estas estructuras, las puede utilizar en muchos contextos de la vida cotidiana.
- Es importante que el alumnado sea consciente de la existencia de esas estrategias y de su proceso de aprendizaje.
- Es importante que el alumnado conozca estructuras que pueda utilizar para resolver los problemas que se le plantean.
Cuando los estudiantes se hacen competentes en el uso de las estructuras, son mucho más capaces de argumentar su razonamiento, de resolver problemas, de enfrentarse a nuevos retos porque sienten que saben dónde se tienen que apoyar.
Os facilitamos unas tarjetas de resolución de problemas para fomentar el trabajo autónomo del alumno. La idea es que el alumno realice cada una de las acciones y pase la tarjeta de un lado a otro para poder hacer sin ayuda del profesor todos los pasos
¡Descarga ahora el material manipulativo para trabajar todo lo aprendido en clases!