Jump Math Blog

En aquesta entrada et donarem totes les claus per treballar els materials manipulatius a les teves classes de matemàtiques de qualsevol etapa educativa. Som-hi!

Segons les investigacions ja no cal demostrar que:

1. Els elements sorpresa tenen incidència directa a la motivació dels alumnes.
2. Un alumne motivat aprèn millor.
3. Els reptes, adaptats al nivell adequat, capten la nostra atenció i ens posen en marxa.
4. L’aprenentatge entre iguals ajuda a tothom.
5. Els materials manipulatius milloren l’aprenentatge.

Per què matemàtiques manipulatives?

Perquè és més que demostrat que milloren i ajuden l’aprenentatge.

Perquè ve al BOE i ho demana la LOMLOE. Utilitzar materials manipulatius està estipulat per llei i hi ha almenys 14 referències explícites tant a l’apartat de primària com de secundària.

Primària:

• Aquesta progressió, que parteix d’entorns molt propers i manipulatius que connecten amb l’etapa d’educació infantil, facilita la transició cap a aprenentatges més formals i afavoreix el desenvolupament de la capacitat de pensament abstracte a l’educació secundària.
• La comprensió de situacions problematitzades no es fa únicament sobre els missatges verbals escrits, sinó que inclou també els missatges orals; els missatges visuals a través de dibuixos, imatges o fotografies; o situacions quotidianes o missatges amb materials manipulatius concrets que suposin un repte.
• Lectura, representació (inclosa la recta numèrica i amb materials manipulatius), composició, descomposició i recomposició de nombres naturals.

Secundària:

• La formulació de conjectures, el plantejament de nous problemes i la seva comprovació o resolució es pot fer per mitjà de materials manipulatius, calculadores, programari, representacions i símbols, treballant de forma individual o col·lectiva i aplicant els raonaments inductiu i deductiu.
• Construcció de figures geomètriques amb eines manipulatives i digitals (programes de geometria dinàmica, realitat augmentada…).
• Transformacions elementals com ara girs, translacions i simetries en situacions diverses utilitzant eines tecnològiques o manipulatives.

Perquè no és jugar, perdre el temps, ni una moda passatgera, sinó que és una manera específica d’aprendre matemàtiques.

Qüestions pedagògiques:

• Perquè tenim el compromís de continuar amb la metodologia a cada etapa educativa. Si a infantil fan servir pràcticament a diari els materials manipulatius, no poden desaparèixer a primària. El mateix passa de primària a secundària. A més, puc ancorar el nou coneixement en un coneixement i material anterior perquè es produeixi l’aprenentatge.
• Perquè és estimulant per a l’alumnat de qualsevol edat, és tan divertit! Als estudiants els agrada molt i divertir-se en matemàtiques també és important.
• Perquè permet adquirir un aprenentatge significatiu i adaptar-se al ritme de cadascú. Si un estudiant necessita utilitzar el material en moltes sessions, cal permetre-ho i adaptar-se al seu ritme.
• Perquè els alumnes són els protagonistes del descobriment de les matemàtiques. Si, per exemple, dono unes peces a l’estudiant i li pregunto: “De quantes maneres es poden col·locar?” Serà l’estudiant qui ho descobreixi i no el docent qui li digui com fer-ho.
• Perquè es treballa en diàleg i en cooperació amb els companys. Si l’estudiant té un material, pot explicar-ho millor als seus companys i explicar-los com pensa a través del material.
• Perquè els alumnes volen que arribi la classe de matemàtiques i la recorden amb gust. Si aprenen amb gust, aprenen millor. Els importa i recorden molt més les classes actives que les classes passives.

Com s’han de portar a l’aula els materials? – El camí cap a allò manipulatiu, on se situa cadascú?

Nivells en què es pot situar el docent a l’hora de fer servir els materials manipulatius:

1. Res de manipulatiu, no sé ni on són les caixes.
2. Tinc el material, sé on és però no l’he tret.
3. Trec el material i el preparo perquè els estudiants puguin fer-lo servir.
4. Faig un taller de matemàtiques un dia fix a la setmana.
5. Dissenyo noves activitats amb materials.
6. Els materials em faciliten la construcció de conceptes nous.

Et convidem a pensar: Tu a quin nivell et trobes ara mateix?

Si encara no teniu material manipulatiu a l’aula, a JUMP Math oferim els següents materials perquè pugueu començar a construir l’aprenentatge des de la manipulació.

Pots saber-ne més sobre ells al següent enllaç: Recursos JUMP Math.

Quan fer servir material manipulatiu?

La resposta és: Sempre! Pots fer-ho:

• A l’inici d’una classe per motivar.
• Durant el desenvolupament de la classe per comprendre (descobriment guiat).
• En fer la pràctica per consolidar.

Com utilitzo el material manipulatiu a l’aula?

Quan dono un material, primer hi ha d’haver una estona de joc. El més normal, abans de començar a realitzar activitats, és que els manipulin, els descobreixin i els investiguin.

Un cop fet això, demanem als estudiants que posin les mans amunt i escoltin les instruccions. Si creiem que serà molt difícil, es pot invertir l’ordre: primer donar les instruccions i després donar material, però és molt important que no manipulin el material mentre escolten les instruccions docents perquè no les escoltaran.

Per últim, ens posem en marxa.

Un material per a cada curs

Et proposem incorporar almenys un material per a cada curs, que podem trobar dins del Kit manipulatiu JUMP Math, i començar a utilitzar-los a les teves classes:

– 1r de Primària – Blocs lògics: És un material lògicament estructurat amb figures geomètriques de diferents mides i colors. És el material per treballar el raonament lògic per excel·lència, des d’infantil fins a cursos avançats de primària. 

Podeu introduir els estudiants mitjançant una festa i hem de saber qui pot i qui no pot entrar a la festa.

Aquesta activitat permet treballar el raonament lògic des de la manipulació, comprenent quan es compleix una condició, quan es compleix l’altra i quan es compleixen les dues condicions.

– 2n de Primària – Bitllets i monedes: Cura, no és un material transparent! No es veu la quantitat que representa. És a dir, si agafo la moneda de 2 euros, tothom sap que per convenció aquesta moneda val 2 euros, però cap nen no pot partir-la i veure que són 2 de res. Si jo per exemple utilitzés 2 boletes, sí que servirien per representar la quantitat, el propi material dona la resposta. Aquest últim sí que seria un material transparent.

Una proposta per treballar amb monedes és agafar un grapat de monedes i ficar-los en una bossa. Sense mirar, treure una moneda i intentar endevinar pel tacte quina moneda és. Quan efectivament comprovo que, per exemple, és la moneda de 5 cèntims, se li proposa a l’alumnat comptar de 5 en 5, de 10 en 10, de 50 en 50. D’aquesta manera, es pot treballar com funcionen les monedes i treballar-hi el compteig. També es pot fer a la inversa, jo compto de 5 a 5 o de 10 a 10 i els nens han d’endevinar quina moneda hauria de tenir a la mà si vull explicar d’aquesta manera.

Una activitat habitual amb diners és pagar amb el mínim nombre de monedes o bitllets

– 3r de Primària – Rellotges: Primer manipulo, després represento i finalment calculo. Els estudiants necessiten manipular per entendre com funciona el temps.

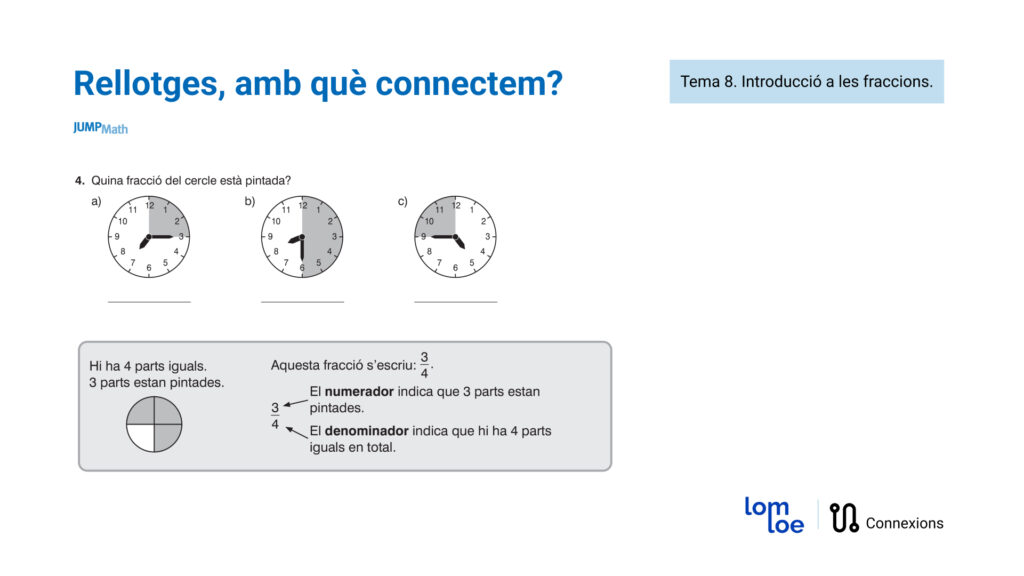
Aquest tipus d’activitats també serveixen per treballar les fraccions, podem situar les busques del rellotge en diferents posicions i veure quina part del rellotge abasten i també podríem fer preguntes del tipus: si una busca marca les 4, on he de posar l’altra per indicar un quart del rellotge? Té aquesta pregunta una única resposta?

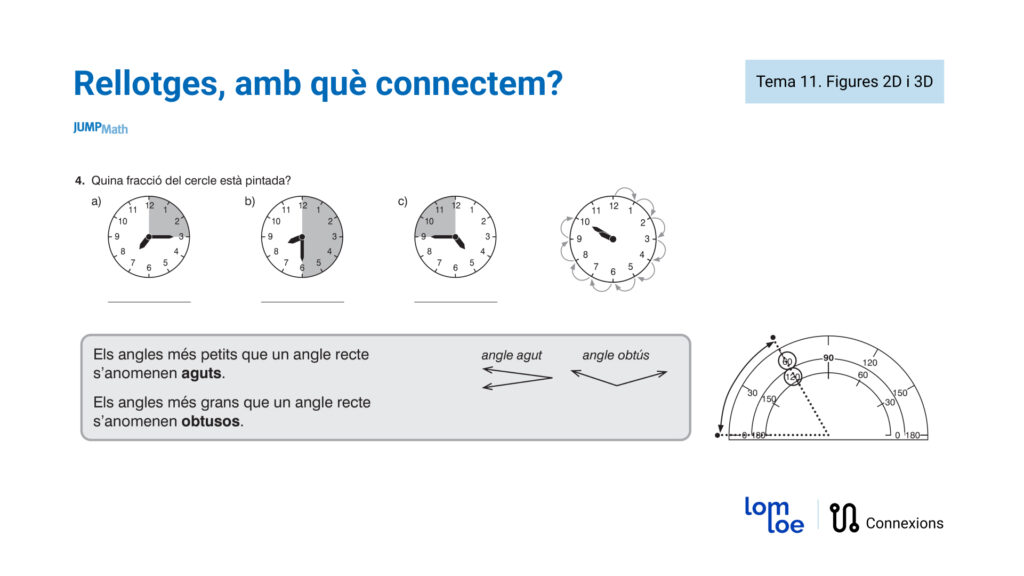
Un altre ús didàctic per als rellotges és treballar els angles. També podem utilitzar el material dels rellotges per treballar els angles. Les dues busques formen sempre un angle (i també el que seria 360º). Per tant, podríem fer servir el transportador d’angles per mesurar-lo.

És interessant perquè en fer servir el mateix material en tres temes tan diferents (hores, fraccions i angles) estem permetent que l’alumnat pugui trobar quina relació tenen i així fer connexions que permetin un aprenentatge més profund.

– 4t de Primària – Geoplà: Permet molt bé els reptes individuals, per parelles i grupals. També es poden utilitzar com a pissarres i a l’hora de contestar aixecar-los per mostrar-ne la resposta.

El geoplà serveix per treballar la geometria plana, per exemple els aspectes següents:

1. Què és un polígon i què no ho és?

Exemple:

2. Tipus de polígons:

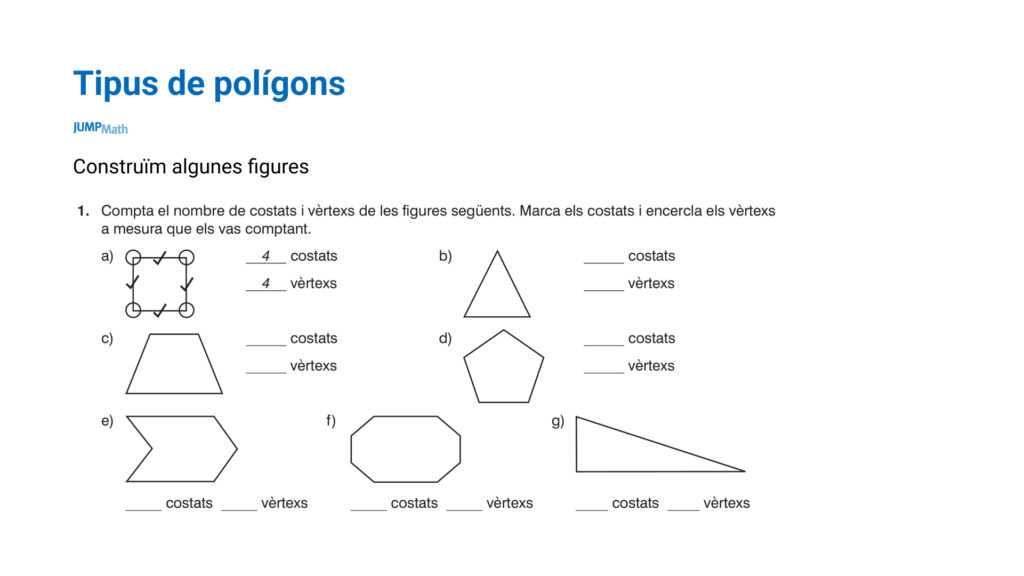
3. Construcció d’angles: Es poden construir angles aguts, obtusos i rectes.

Exemple:

4. Construcció de rectes paral·leles i perpendiculars: Es poden proposar reptes com “Construir línies perpendiculars i paral·leles, però que no siguin verticals ni horitzontals, sinó obliqües”.

Exemple:

Altres reptes que es poden dur a terme són:

• Quins polígons regulars puc construir al geoplà?
• Quants quadrats “diferents” puc fer? (entenent en aquest cas com a “diferents” de costats sencers o costats irracionals)
• Quins quadrilàters es poden construir al geoplà?
• Construir polígons donat un nombre de costats o, a la inversa, anomenar polígons construïts per altres.

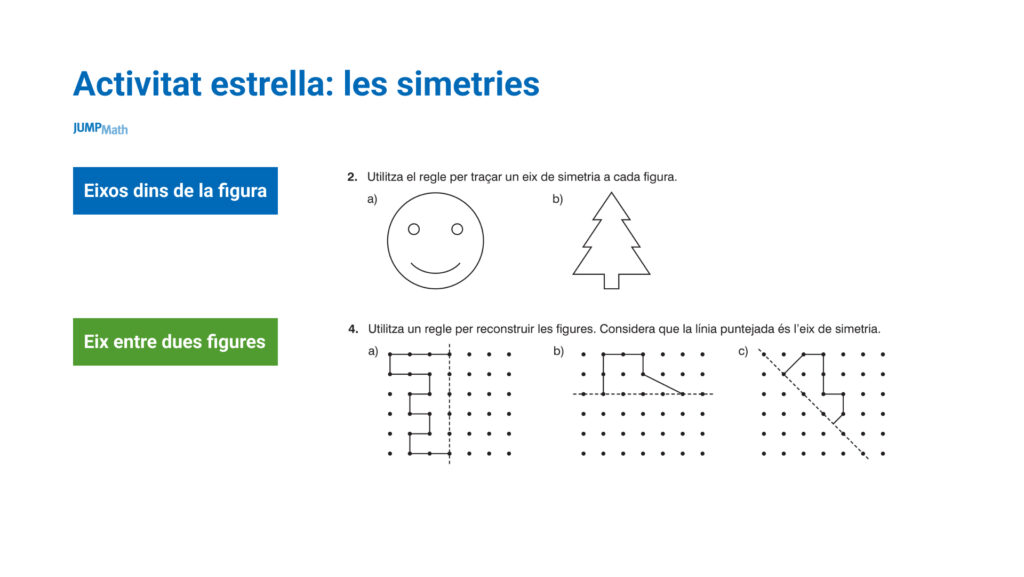
L’activitat estrella dels geoplans són les simetries o bé perquè li dono l’eix de simetria i cal construir una figura, o perquè li dono una figura i s’han de trobar els eixos de simetria.

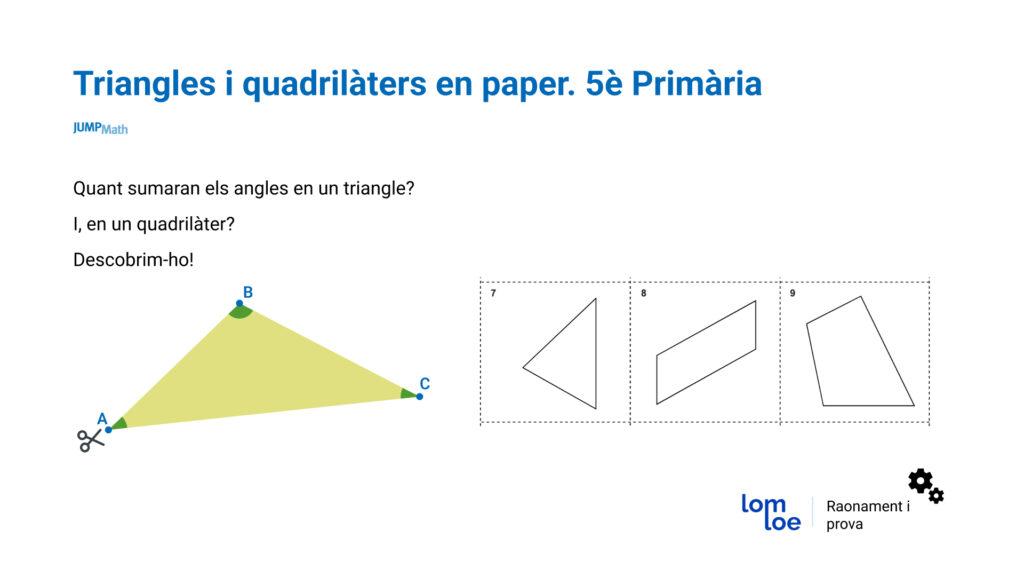
– 5è de Primària: Polígons retallables en paper: Aquesta activitat no parteix d’un material manipulatiu JUMP Math però sí d’una de les activitats. Demanem als estudiants que retallin un triangle i un quadrilàter (el que vulguin) i que vegin quant sumen els angles interiors. És important que ells mateixos escullin aquestes figures perquè vegin que aquesta condició no es compleix només per a unes figures prèviament dissenyades. A continuació es demana als estudiants que retallin les puntes i les uneixin pels vèrtexs perquè puguin veure que efectivament, en ajuntar-los, es forma un angle pla de 180º.

– 6è de Primària: Blocs multibase: S’utilitzen molt a primària per construir les desenes.

Amb elles es poden realitzar operacions:

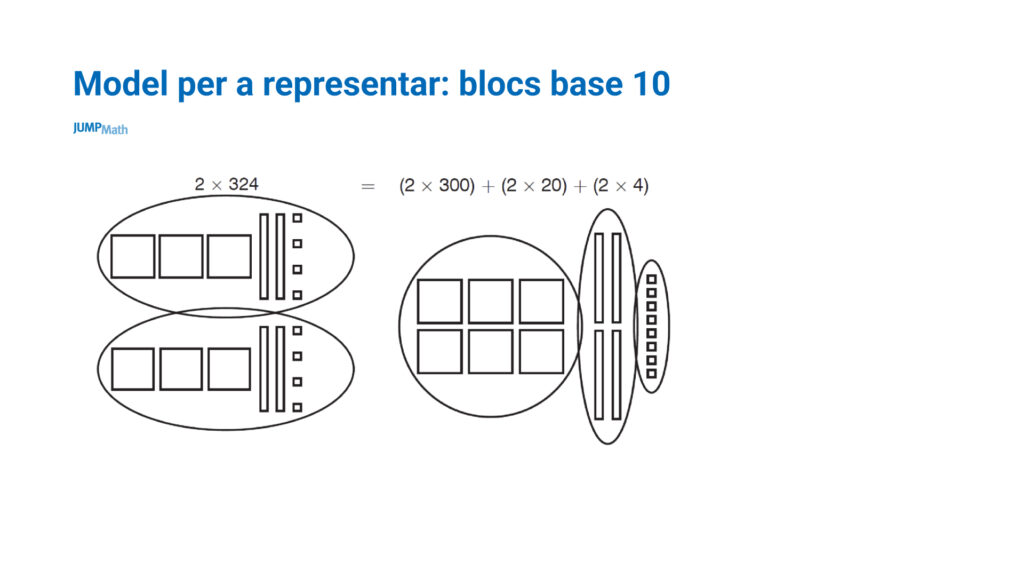
Són interessants per canviar el punt de vista, en lloc de dir: 1, 10, 100, es pot presentar la placa de centena com a unitat, la barra de deu com una barra de desena i el bloc d’unitat com a centèsima.

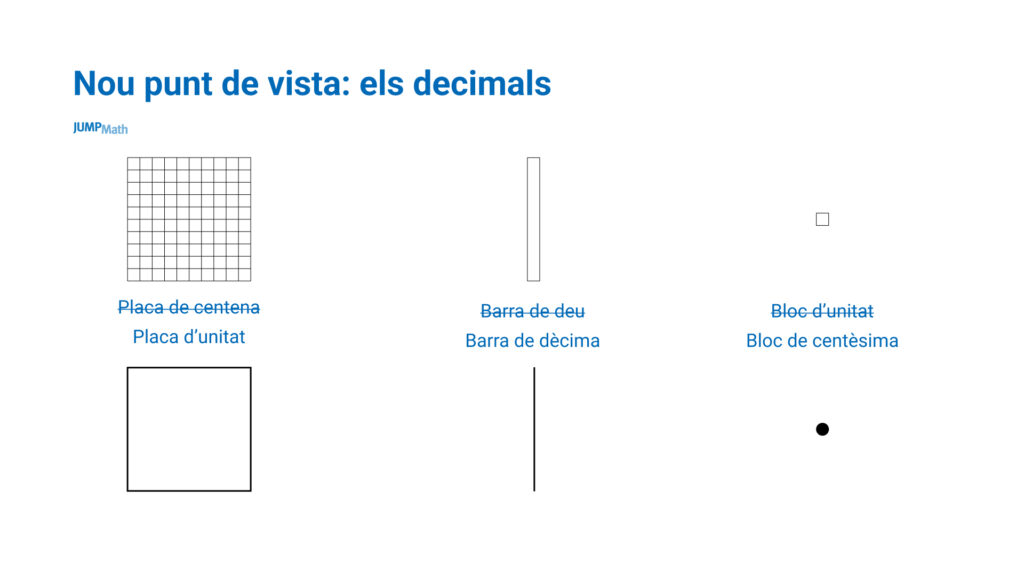
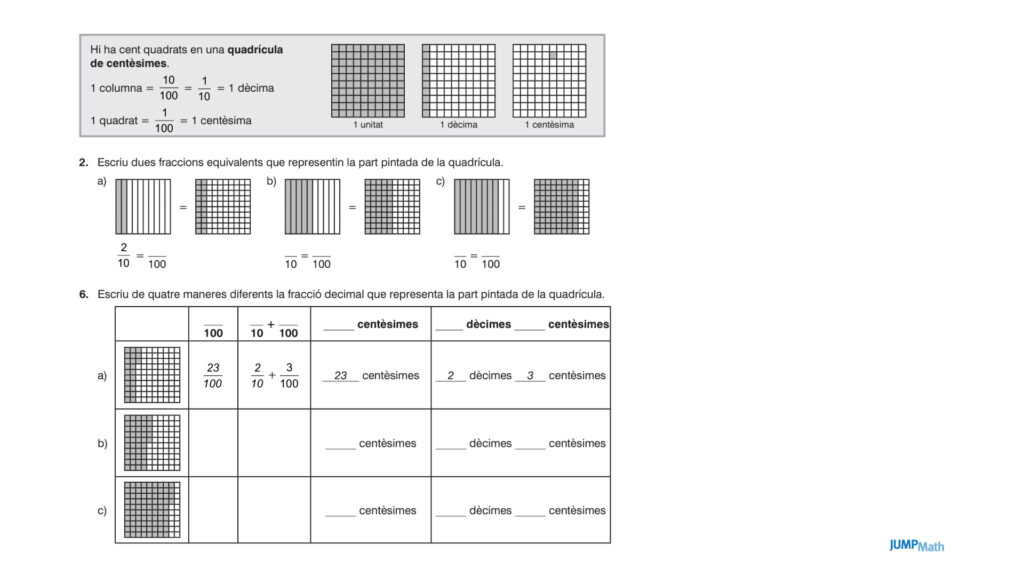
També, mitjançant aquest material, es poden ensenyar els percentatges:

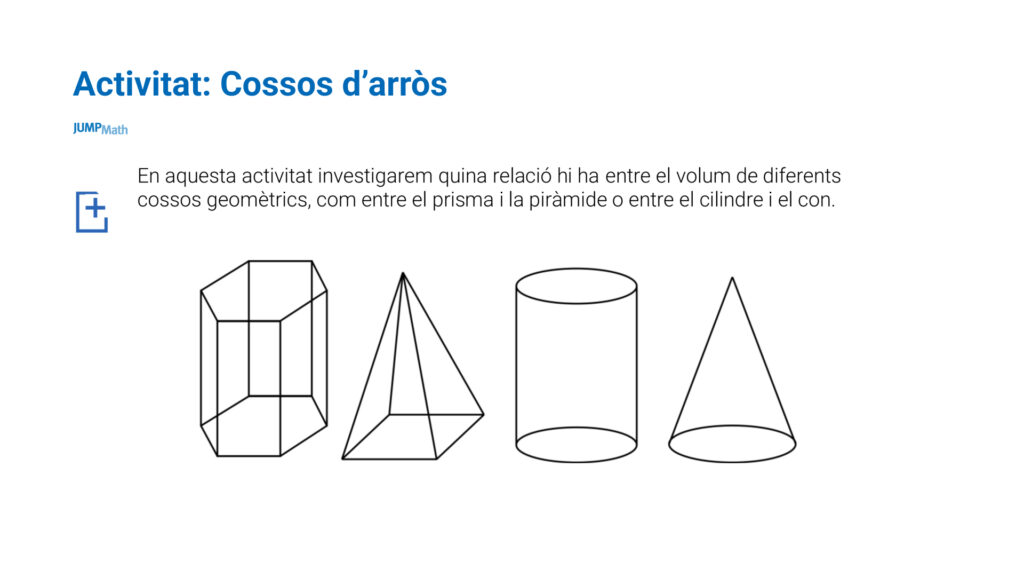
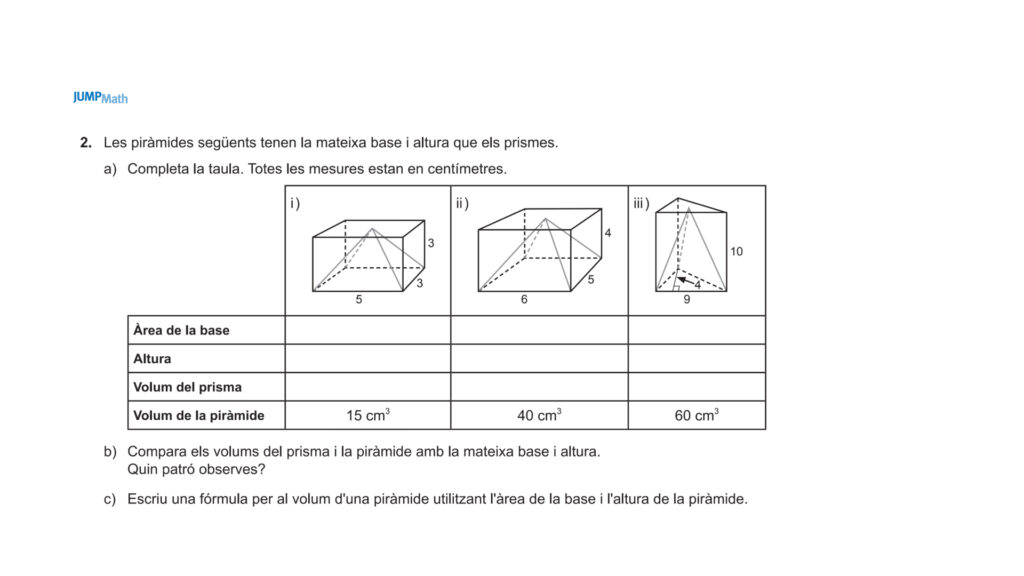
– 1r i 2n de l’ESO – Cossos geomètrics: Els cossos geomètrics estan pensats perquè tinguin relació els uns amb els altres. D’aquesta manera es pot calcular el volum dels cossos, omplint-los d’arròs o aigua. Així podreu veure que, per exemple, amb l’arròs que omple 3 piràmides, s’omple un cub, i podran experimentar ells mateixos que el volum d’un con és la tercera part del volum d’un cilindre.

Exemple:

En resum:

• Els materials serveixen per a qualsevol etapa educativa.
• Per a cada contingut podem trobar-hi un material.
• Els materials ajuden a construir el coneixement.
• Els materials posen l’alumne com a protagonista de l’aprenentatge.
• Els materials han de ser accessibles.
• Motiveu l’alumnat!