Prepárate para que el alumnado del año que viene se entere de los enteros desde el minuto uno. ¡No más dramas con los números negativos! Empecemos…

¿Por qué son importantes los enteros?

1. Requiere tener conocimientos previos sobre números naturales:

• Se necesita que el alumnado sepa situarlos en la recta real.
• Saber comparar y ordenar.
• Saber realizar operaciones.

2. Son esenciales para otros contenidos:

• Cálculo con racionales e irracionales.
• Trabajo con monomios.
• Resolución de ecuaciones, inecuaciones y sistemas.
• Trabajo con funciones, situar puntos en los ejes de coordenadas.

Estos son contenidos que se ven a lo largo de la secundaria y bachillerato y que se apoyan directamente en lo aprendido en los números enteros.

3. Es el tema nuclear en primer ciclo de ESO:

• Se hace necesario un trabajo profundo.
• “Menos por menos es… menos”. Este tipo de frases impiden un buen aprendizaje. La mecanización hace que los estudiantes no entiendan realmente lo que están haciendo, que no sean capaces de argumentar sus propios razonamientos y se les está enseñando que las matemáticas son una especie de “magia” que si la aplicas te va a ir bien. Esto hace que no sepan dónde se están equivocando.

¿Qué traen de nuevo los enteros?

Es importante, cada vez que aparece un nuevo conjunto numérico en clase, preguntarse: “¿qué aporta este nuevo conjunto que no aportaban los conjuntos numéricos que se venían trabajando?, ¿en qué son diferentes?, ¿en qué son iguales?, ¿qué estructuras se mantienen y cuáles no?” para que esa reflexión permita comprender que en algunas cosas se parecen al conjunto anterior pero en otras cosas no.

Aparece un nuevo conjunto numérico, ¡no es cualquier cosa!

1. Opuesto: 

–Permite representar realidades contrarias. El alumnado podrá representar, por ejemplo, cuando algo se encuentra sobre el nivel del mar, pero también cuando algo se encuentra bajo el nivel del mar.

– Cantidades con signos positivos y negativos. Cuando se trabajan únicamente los números naturales no hacía falta poner su signo correspondiente, pero ahora sí.

-Todo número tiene su opuesto. 

2. Representación:

• Se necesita toda la recta real para poder representar los opuestos.

• Números opuestos son simétricos respecto al cero. Esta simetría permite comprender los números opuestos desde otra perspectiva.

3. Valor absoluto:

• Si dos números tienen el mismo valor absoluto pueden ser el mismo o ser opuestos. Antes, con los números naturales, si dos números tenían el mismo valor absoluto, eran exactamente el mismo número. Ahora, podrá ser el mismo número o su opuesto.

• Tener mayor o menor valor absoluto no determina si el número es mayor o menor. Con los números naturales, si uno tenía mayor valor absoluto que otro, significaba que el número era mayor. Ahora, con la incorporación de los números negativos, esto ya no es así. 

4. Comparación y orden:

• Un número puede tener mayor valor absoluto que otro y sin embargo estar a la izquierda en la recta real (ambos negativos).

5. Descomposición en suma:

• Cada número se puede descomponer como dos sumandos de infinitas formas. Al contrario de los números naturales que cada número se puede descomponer como suma de dos sumandos una cantidad finita de veces. 

6. Operaciones:

•  Al sumar dos números, el resultado puede ser menor y al restar puede ser mayor. 

• Puedo restarle el número mayor al menor.

• Al multiplicar, el resultado puede ser menor y al dividir, mayor.

Nuevos (clásicos) contextos de los enteros

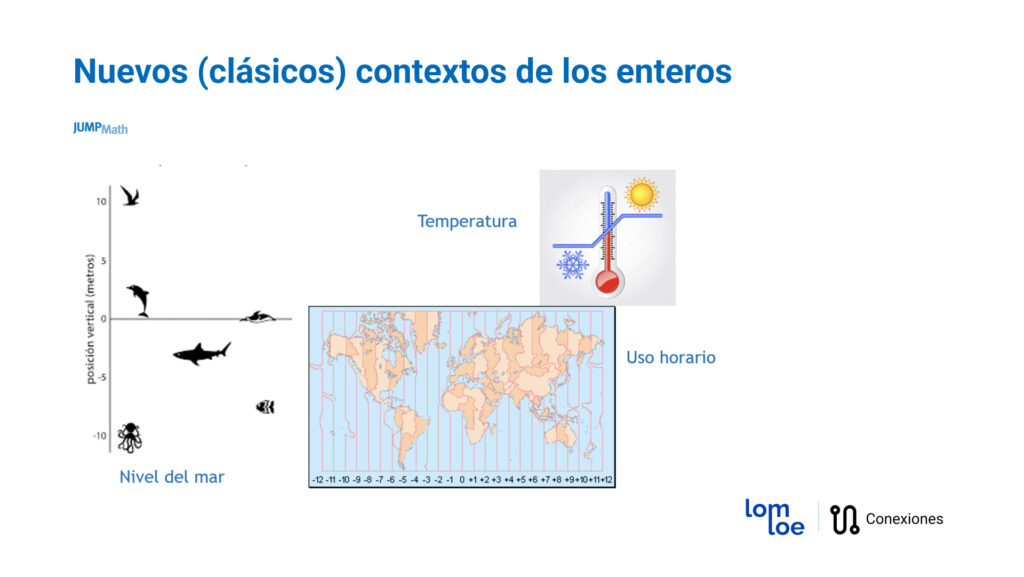
Son nuevos ya que con los números naturales no se podían representar, pero a la vez son clásicos porque son ejemplos comunes en clase.

Resolución de problemas. Representar para solucionar.

Los alumnos están tan acostumbrados a que para resolver problemas hay que hacer operaciones que muchas veces representan si se lo pides pero luego no usan esa representación para resolver el problema. Es fundamental hacer un trabajo específico de cómo puedo usar la representación para obtener la respuesta que busco.

Otros contextos: cantidades que se anulan

Otros contextos distintos donde la representación en la recta real no nos ayuda tanto serían los contextos donde las cantidades se anulan como cuando hablamos de dinero, de pérdida, de ganancia, de puntos, de saldos, etc…aquí es mejor usar los modelos que veremos a continuación de cargas positivas y negativas.

¿Cuándo se denominan opuestos?

Dos números se denominan opuestos entre sí, cuando ambos están a la misma distancia de 0 pero en sentidos contrarios. Podemos aprender cómo funcionan los opuestos haciéndoles diferentes preguntas:

• ¿Cuál es el opuesto de -3?
• ¿En qué son iguales los números opuestos?
• ¿En qué son diferentes a la hora de escribirlos?

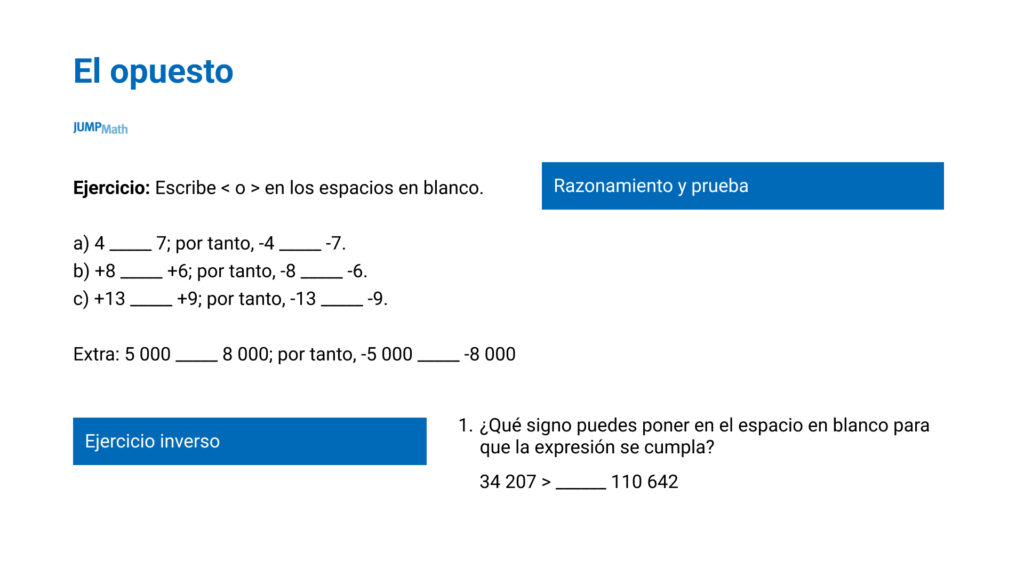
Ejercicios de razonamiento y prueba: Estos ejercicios son interesantes ya que los estudiantes pueden ver que si 4 es menor que 7, entonces automáticamente podré saber que – 4 es mayor que – 7.

Ejercicios inverso: El estudiante puede ver que si pone un más, no se va a cumplir pero si añade un -, sí se cumple.

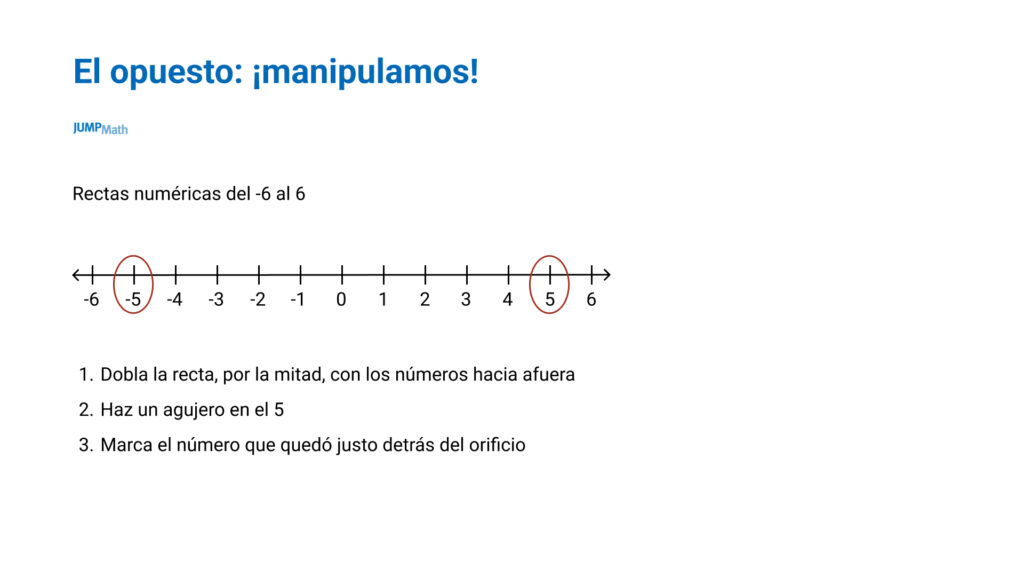
Los opuestos también se pueden entender manipulando:

Las 4 operaciones

Sumar números enteros

• Conjetura 1: Pérdidas y ganancias. 

• Conjetura 2: Determinar el resultado total de una pérdida y una ganancia.

• Conjetura 3: Determinar el resultado total de dos ganancias y dos pérdidas.

En este tipo de actividades, se están sumando números enteros sin la idea de realizar operaciones, sino más bien en contextos dónde los estudiantes de forma natural pueden llegar al resultado.

Pasos para trabajar con números enteros

• Usamos material manipulativo: Fichas rojas y azules. Con ellas se pueden realizar todo tipo de actividades:

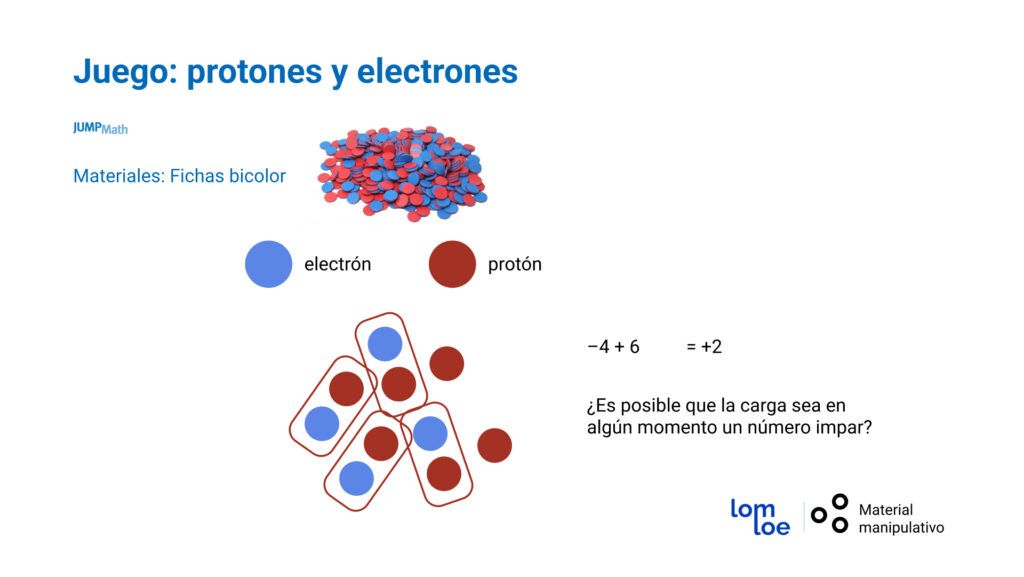
Entonces el signo + va a representar ganancia o carga positiva. Y el signo – va a representar pérdida o carga negativa.

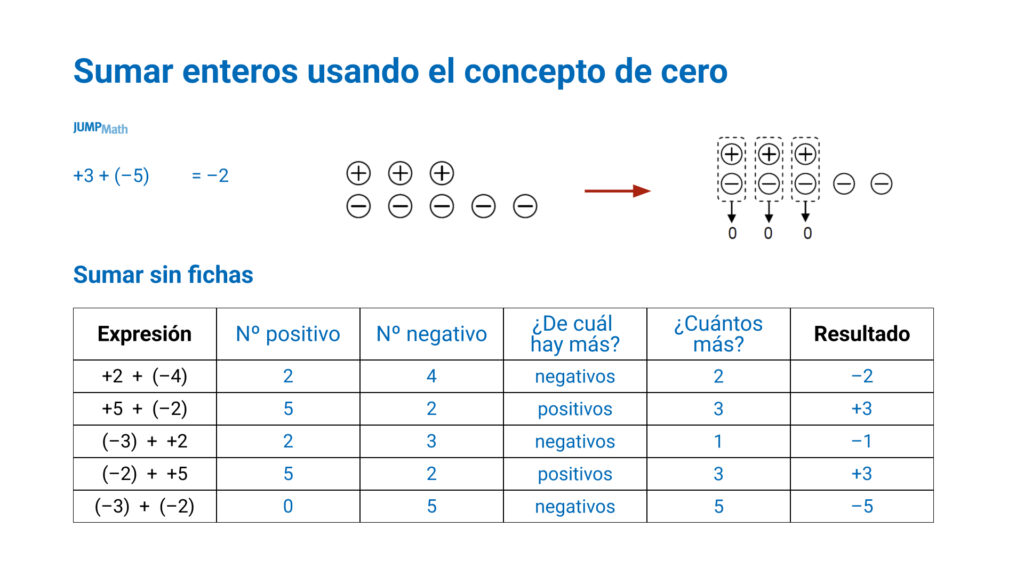
Es importante dar ejemplos dónde los estudiantes puedan ver que da lo mismo si las cargas positivas están por delante o por detrás porque lo importante es cuántas tienen.

• Representamos: Sumar números enteros en la recta numérica.

Se sumarán números enteros relacionándolo con el movimiento.

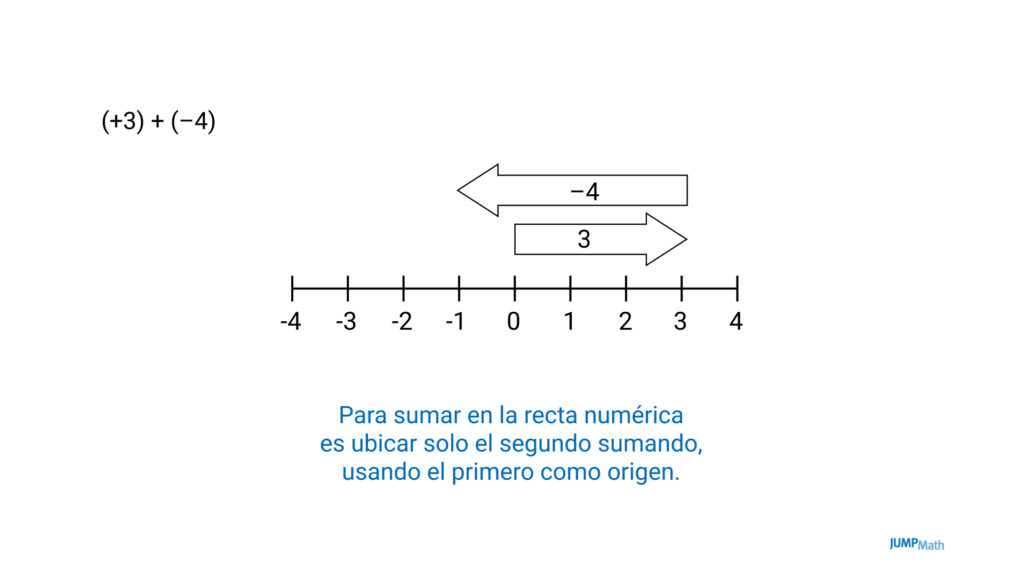
Ambas representaciones son muy importantes porque es una forma de aprender lo mismo de distintas formas y de esta manera se atiende a la diversidad a la vez que se favorece que el alumno tenga una comprensión más global del concepto que estamos tratando.

• Operamos simbólicamente: Usamos diferentes métodos.

Cuando lo que hay que sumar son más de dos pérdidas o más de dos ganancias hay distintos métodos: 

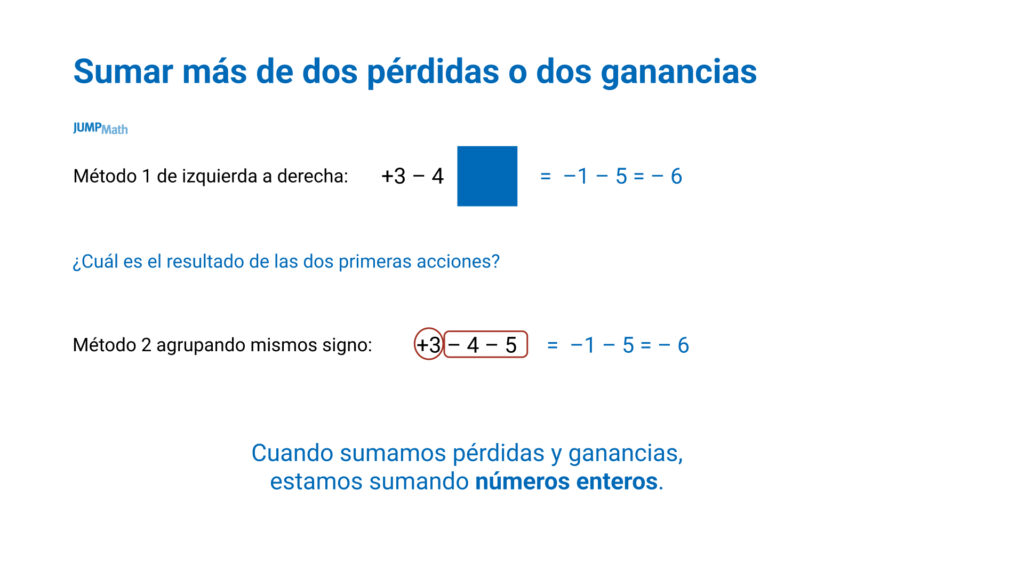
Estos métodos no necesariamente deben ser sucesivos, sino que se pueden combinar.

Restar números enteros

Itinerario de la resta: 

• Comenzamos restando positivos entre sí o negativos entre sí, porque esta resta se parece mucho a los números naturales respecto al concepto de “quitar”.
• Aprendemos a escribir los números de muchas maneras. ¿Cómo decir sin decir? Se puede decir 3 o 4 + (-1).
• Añadimos cargas neutras. 

Restar números con el mismo signo.

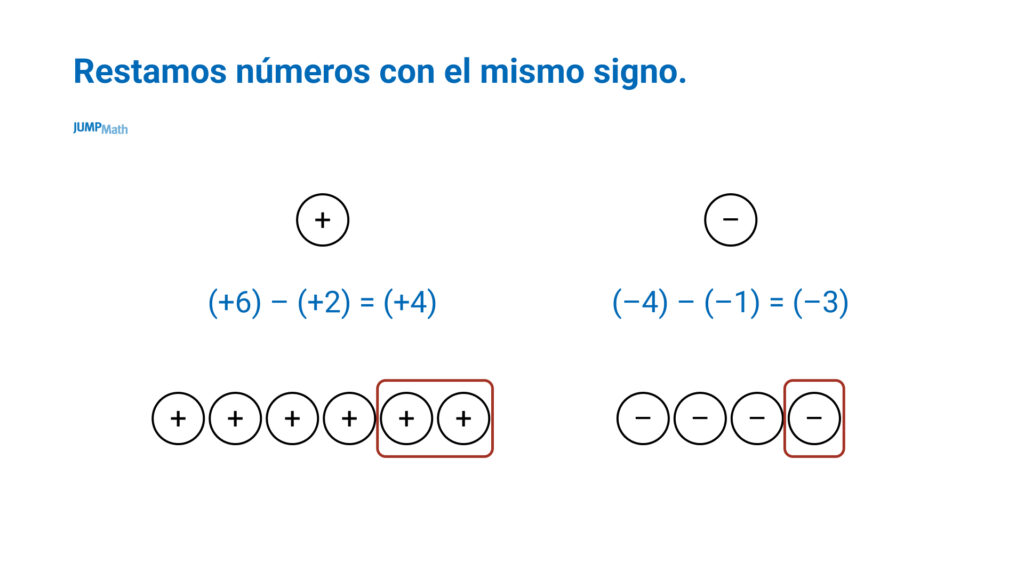
En estos casos es muy importante el lenguaje, ya que por lo general cuando los estudiantes tienen dificultades es porque están pensando en operar, en lugar de pensar en cargas negativas y cargas positivas. Ser claros en el lenguaje, facilita la comprensión de la actividad. 

Por eso es importante que tengan una representación tanto manipulativa como pictórica previa a la representación simbólica.

Representar el mismo número de muchas maneras. 

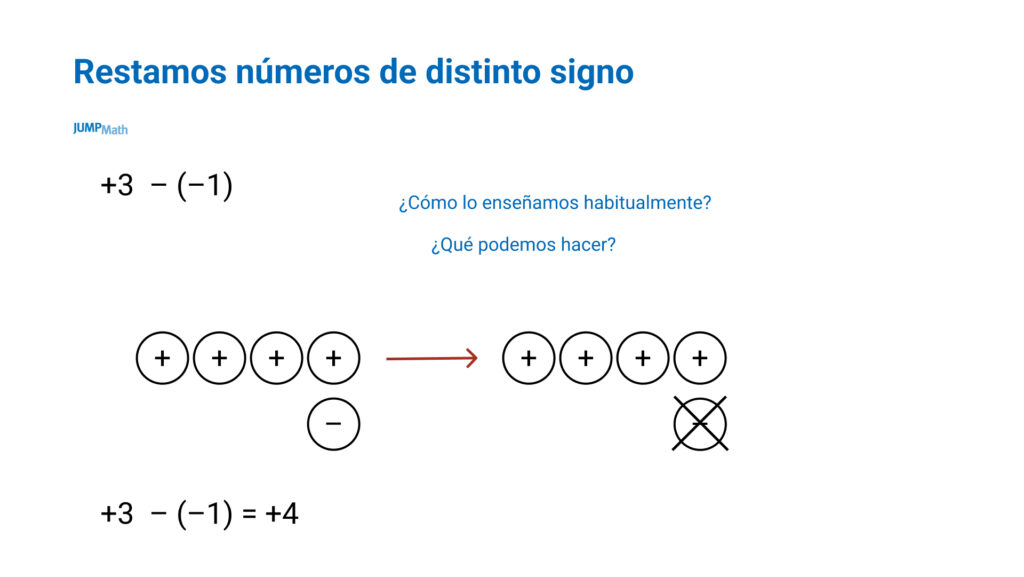
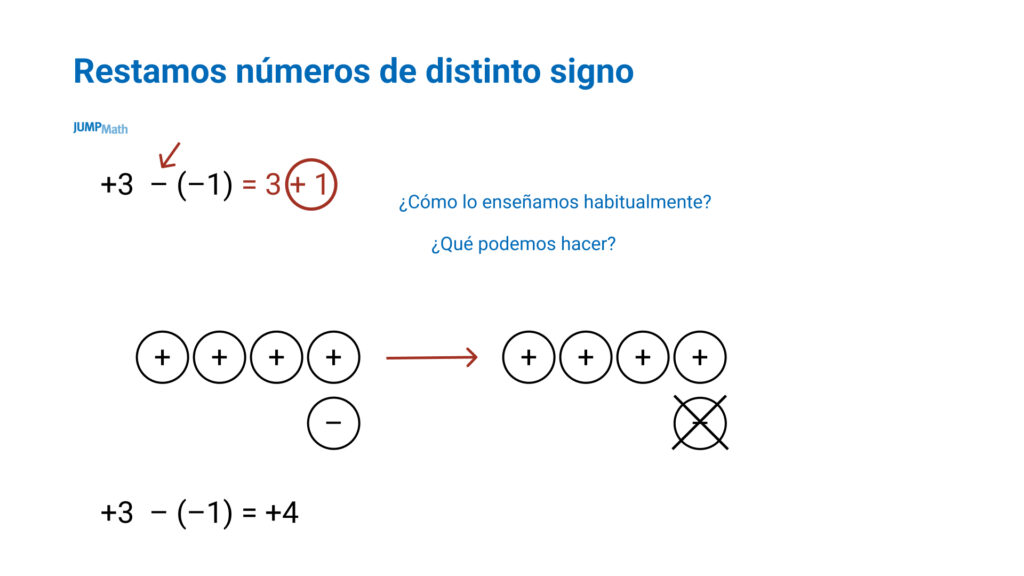
Restar números de distinto signo

Esto es lo que más le cuesta a los estudiantes porque no se puede entender cómo voy a quitar una carga negativa si solo tengo carga positivas. Por tanto, lo que tenemos que hacer es expresar el número de una nueva manera de forma que sí haya cargas negativas que quitar.

El 3 se puede expresar como 3 cargas positivas, pero también se puede expresar como 4 cargas positivas y 1 negativa.

Resta de números con mismo signo pero insuficiente cantidad

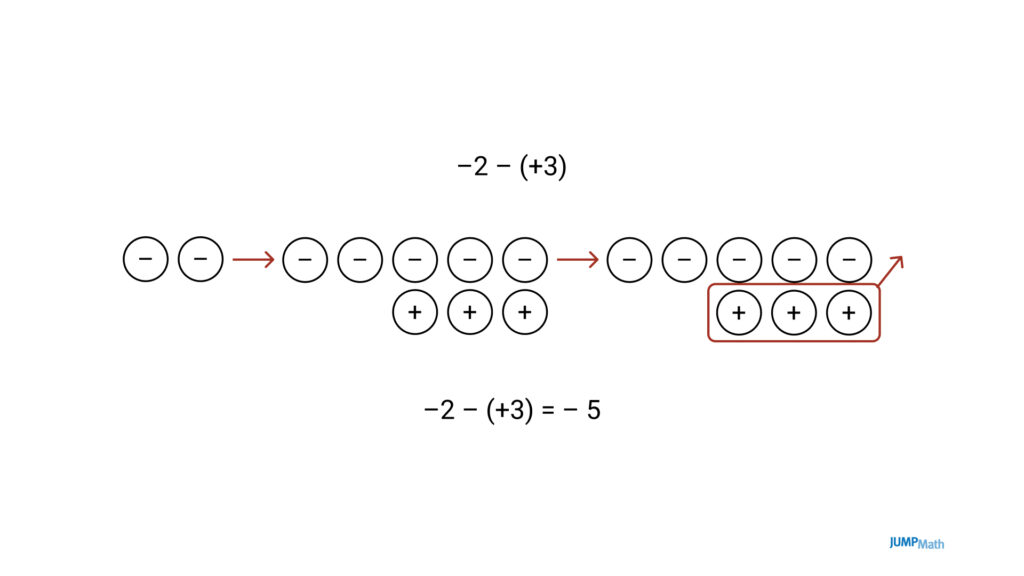
Cuando por ejemplo, tengo dos cargas negativas y quiero quitar tres cargas positivas, se añaden 3 cargas neutras (tantas como quiera quitar) y quedarían entonces 5 cargas negativas.

Proceso inverso

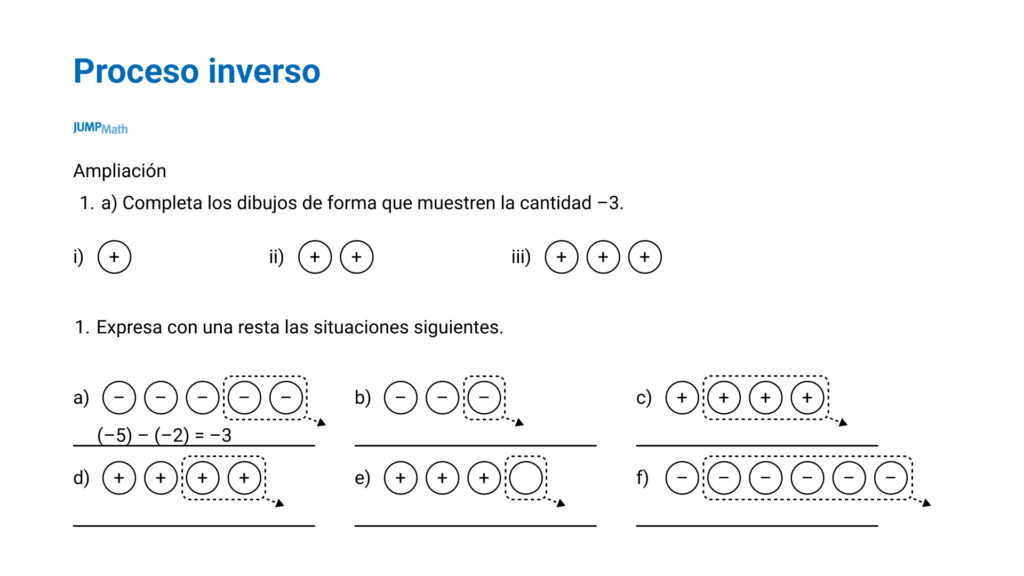
También se puede hacer el proceso inverso: Escribir la operación que está representada pictóricamente.

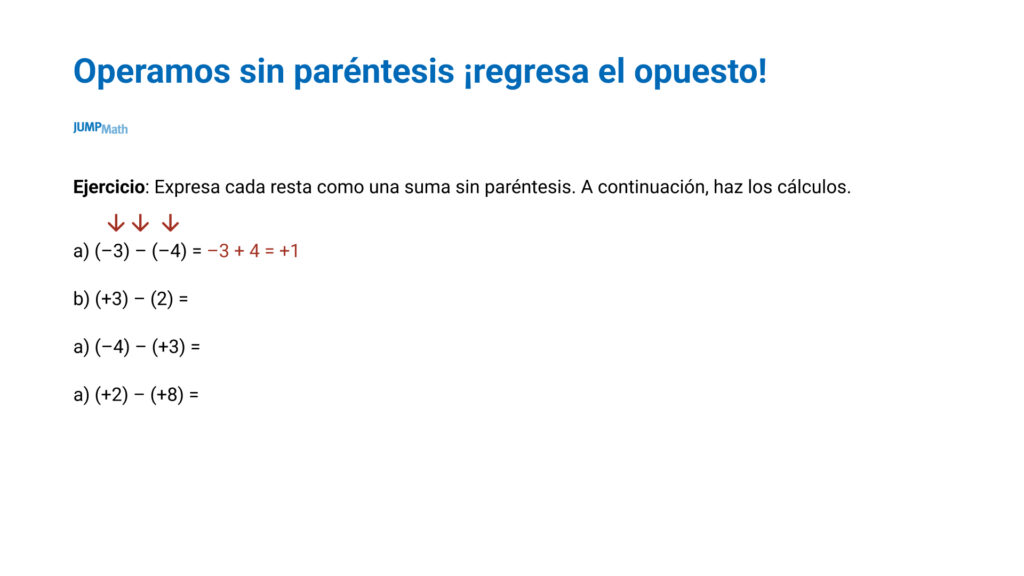
Operamos sin paréntesis ¡regresa el opuesto!

Otra alternativa es regresar al opuesto y transformar todas las restas en sumas, ya que es algo que los estudiantes saben hacer bien. 

Multiplicar números enteros

Propuesta 1: La multiplicación como suma abreviada

Es muy importante no explicar nada a los estudiantes que ellos puedan construir y deducir. Entonces el docente se dedicará a ofrecer cuestiones como si no supiera nada, para ver qué hacen los estudiantes.

Se puede partir de las multiplicaciones de números naturales, que es algo que sí saben hacer. 

Propuesta 2: Modelo rectangular a x (-b) con a x b

Cuando yo multiplico a x b, lo que se consigue es el área. Entonces, se puede partir de allí para plantear que si hay un rectángulo de base 5 y altura – 3, pues tendría 15 de área pero en la parte negativa y comprobarán nuevamente la propiedad conmutativa de la multiplicación.

Propuesta 3: Descubrir patrones

Otra posibilidad es deducir las reglas de la multiplicación gracias a la observación de patrones. A medida que voy multiplicando por un número más bajo el resultado va aumentando.

Esto no es por haberle dicho al alumnado que – x – es +, sino que lo van descubriendo ellos mismos y van encontrando el sentido.

Dividir números enteros

Comprendemos la operación inversa. Familias de enteros. 

A la hora de dividir, se aplica lo mismo que multiplicar.

Resumen

• Los números enteros son un tema central. Sobre todo en la última etapa de primaria y la primera etapa de secundaria, porque hacen de nexo entre muchos contenidos.
• Es un nuevo conjunto numérico que hay que conocer cómo funciona y diferenciarlo de los números naturales para diferenciar qué características se mantienen y cuáles no. 
• Manipular y representar permite comprender cómo funcionan. Es fundamental empezar manipulando y representado.
• Las operaciones pueden hacerse desde diversas perspectivas. Desde la perspectiva de anular cantidades, desde la perspectiva de utilizar la recta numérica y el movimiento, la búsqueda de patrones, etc.

Conviene realizar un aprendizaje profundo. No un aprendizaje mecánico, para que puedan razonar y entender los por qué. Por eso es importante plantearlos desde el descubrimiento y las distintas estructuras y propuestas. Que tengan que enfrentarse a retos constantes.